組み分け

カテゴリー：数学A

6人から2人を選ぶ場合、並び順を考慮しなくて良いのであれば、組み合わせの公式を使い、

から、15通りであることがわかる。

では、6人を2人ずつの3チームに分ける場合はどうなるだろう？

この場合は、6人から2人選んだあとも選び続けなくてはならない。

このようなときに組み分けの公式を使って解いていく。

基本的には、組み合わせを理解していれば簡単に理解することができる。

(1)6人を2人ずつのチームA, B, Cに分ける。

(2)6人を2人ずつのチームに分ける。

この2つの問題は意味が違うのである。

組み分けの問題を解くときにまず考える必要があるのは、分けるものが区別できるかどうかである。

(1)の場合はチーム名がついているので、区別することができる。

つまり、チームの並び順を考慮する場合である。 （ここで、チーム内での並び順は考慮しなくていいことに注意する。

(2)の場合は、チーム名がついていないので、区別することができない。よってチームの並び順は考慮しなくていい。

(1)の場合(チームの並び順を考慮する場合)

まず、チームAは6人から2人を選ばなくてはいけないので、\( {}_6 \mathrm{C}_2 \)。

次にチームBは2人引いた4人から2人選ぶので、\( {}_4 \mathrm{C}_2 \)。

最後は、2人から2人選ぶので、1通りしかない。

これら3回のチーム分けは同時に起こるので、掛け合わせることで、

より、90通りあることがわかる。

(2)の場合(チームの並び順を考慮しない場合）

(1)ではチームの並び順を考慮したが、(2)では考慮しない。

6人をここではa, b, c, d, e, fとする。

(1)では、{a, b}、{c, d}、{e, f}と分けた場合は、図1のようにA, B, Cの6通りの分け方が考えられた。

つまり、3!通りの分け方があったのである。

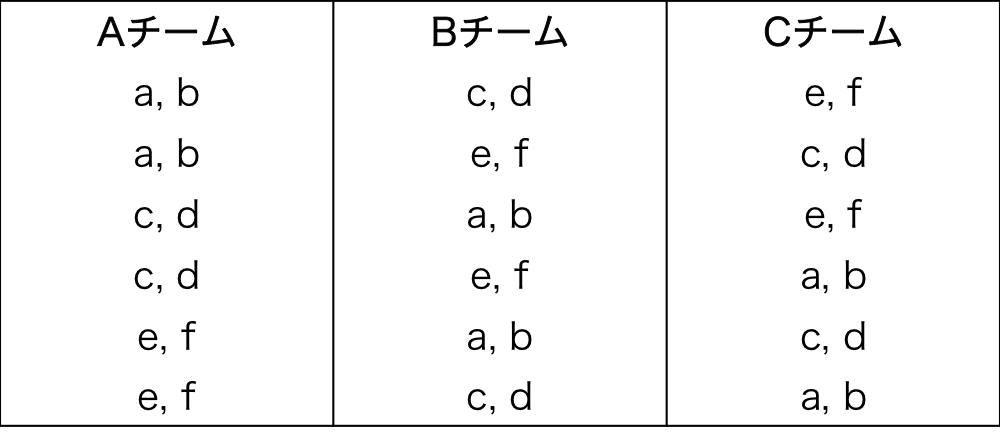
図1.

(2)の場合は、チームの区別はなくなるので、同じものができてしまう3!（3チームの並び方）分だけ割ってやればいい。

つまり、

より、15通りである。