樹形図

カテゴリー：数学A

何通りかの場合を考えなくてはならない時、すべてを頭に思い浮かべて導き出すことは難しい。

2通りとか5通りくらいならなんとかなるが、場合の数が増えれば増えるほど難しくなってくる。

そこで、何通りあるかをすべて書き出して数える図を作成することが有効である。

この図のことを樹形図と言う。

では、どのような場合に樹形図が有効であるか考えていく。

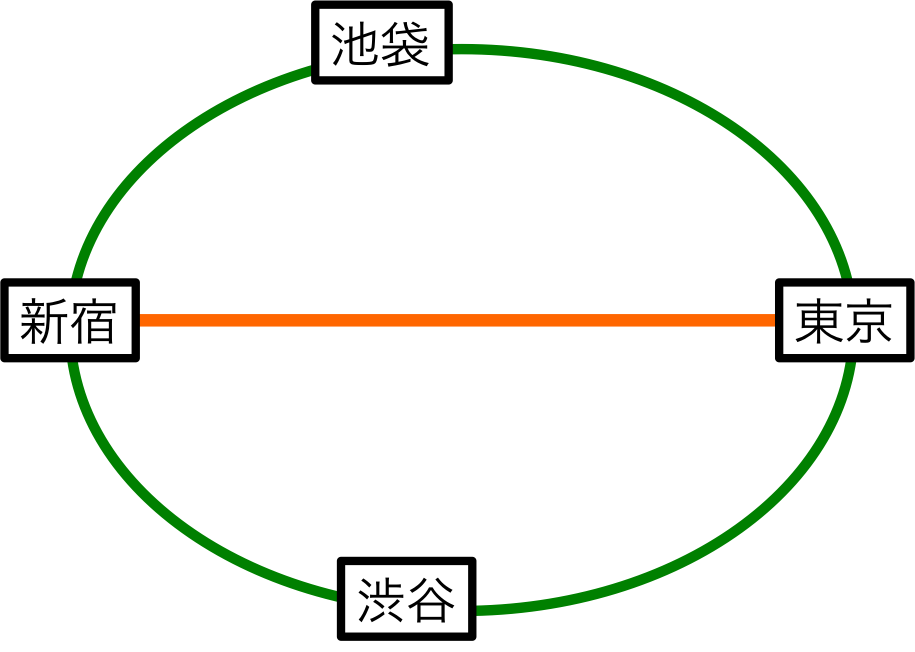
図1.

東京観光する場合を考えてみる。

図1のような路線を使って、新宿駅を起点に、渋谷、池袋、東京などの駅を観光しようと思う。

この路線は全ての駅が緑の環状線上にあり、新宿駅と東京駅はオレンジの路線でつながれている。

この路線図を使って、新宿駅を出発して再び新宿駅に戻ってくるには何通りのプランが考えられるだろう？

ここで、新宿を出発し、再び新宿駅に着いたら旅行は終了するとし、他の駅には2回以上行かない。

まず考えられるのは、新宿駅から東京駅、渋谷駅、池袋駅に行きそのままUターンして新宿駅に戻ることである。

これは簡単で3通りのプランが考えられる。

次に、緑の路線を使って、新宿→渋谷→東京→池袋→新宿と言う、環状線１周プランも考えられる。

ここまでならなんとか頭で考えられるが、これ以上の場合になると混乱してきてしまう。

では、頭で考えるのではなく、図を書いて考えてみようと思う。

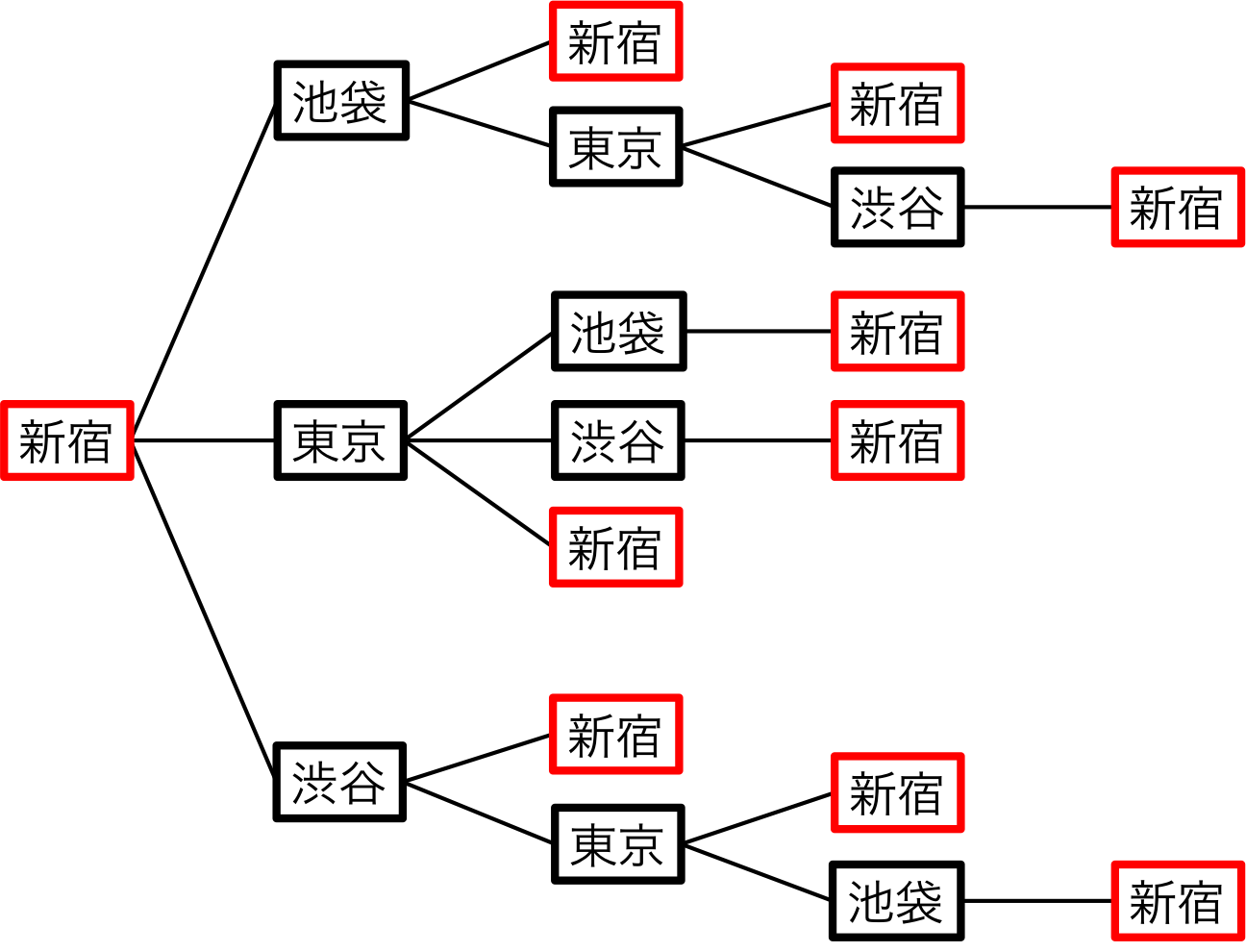
図2.　樹形図

新宿を起点とすると、次に向かう駅は、渋谷駅、東京駅、池袋駅が考えられる。

池袋駅に行くと、次は新宿駅に戻るか、東京駅に行くかの場合が考えられる。

3列目に着目すると、池袋駅から新宿駅に向かった場合はそこでプランは終了となるのだが、 東京駅に向かった場合はまだ、新宿に戻るか渋谷に行くかの場合が考えられる。

このように起こり得る全ての場合を、右から左に向かって書いて行き、線で繋ぐこの図を樹形図と呼ぶ。

樹形図によって、この東京観光には9通りのプランが考えられることがわかるのである。

「新宿を終着駅にする」や「同じ駅には2回以上行かない（重複しない）」と言った条件が存在する順列や組み合わせの場合の数を全て書き出す時に、樹形図は非常に有効である。

逆に、20人の並べ替えなど、書き出す量がものすごく多くなってしまう場合は樹形図で解くことはおすすめしない。