和集合の要素の個数

カテゴリー：数学A

全体集合\( U \)があり、その部分集合\( A \)、\( B \)があり、 \( A \)と\( B\)の要素数が、

\begin{align} n(A) &= a \\ b(B) &= b \end{align}

であるとする。

ここでは、\( A \)と\( B \)の和集合の要素数がどうなるのかを考えていく。

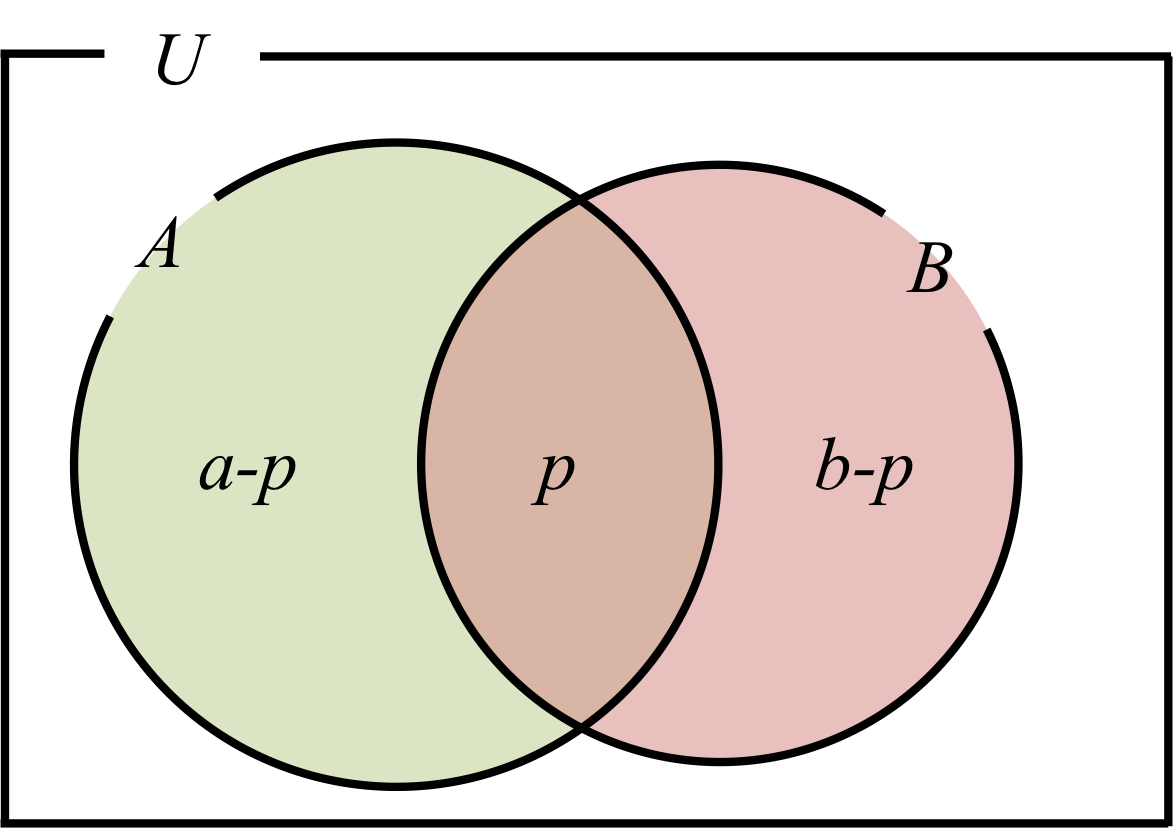
図1.

この場合、集合\( A \)と集合\( B \)が共通部分を有する場合と有さない場合の2つの場合が考えられる。

集合\( A \)と集合\( B \)が共通部分\( A \cap B \)を有する場合

共通部分の要素数が、

\begin{eqnarray} n (A \cap B) = p \end{eqnarray}

である時、図1のようになる。

\( A \)から\( A \cap B\)を除いた\( A \cap \overline{B}\)とBから\( A \cap B\)を除いた\( \overline{A} \cap B\)の要素数は

\begin{align} n ( A \cap \overline{B} ) &= a - p \\ n (\overline{A} \cap B ) &= b-p \end{align}

となる。よって、\( A \)と\( B \)の和集合\( A \cup B \)は、

\begin{align} A \cup B &= A \cap \overline{B} + \overline{A} \cap B + A \cap B \\ &= (a-p) + (b-p) + p = a+ b -p \end{align}

となる。このことから、

\begin{align} A \cup B &= n(A)+n(B) - n( A \cap B) \end{align}

であることがわかる。

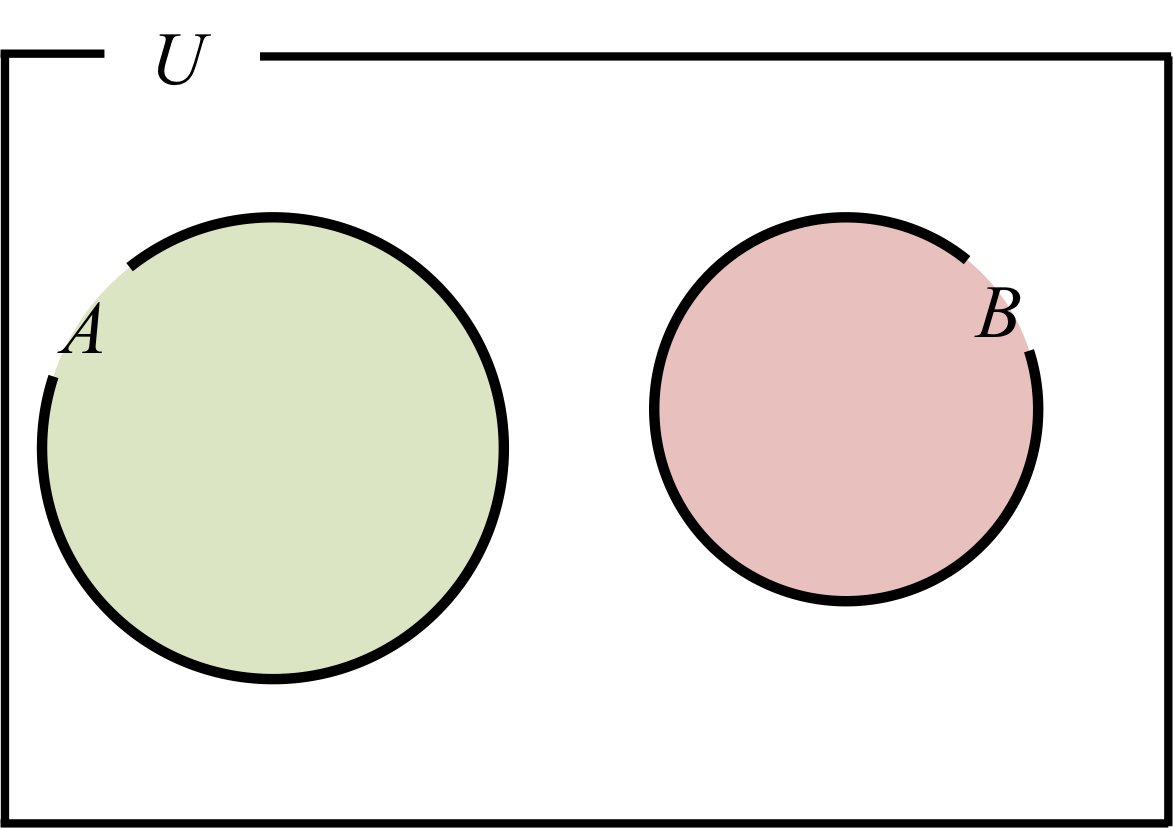
図2.

\( A \)と\( B \)に共通部分がない場合（\( A\cap B = \varnothing \)）

この時は簡単に、

\begin{align} A \cup B = n(A) + n(B) \end{align}

とできるのである。