ド・モルガンの法則

カテゴリー：数学A

集合\( A \)と集合\( B\)の共通部分と和集合である、\( A \cup B \)と\( A \cap B \)の補集合について、 次の法則が成り立つ。

この法則をド・モルガンの法則と呼ぶ。

ド・モルガンの法則が主に効果を発揮する場面は、プログラムを作成する場合である。

高校数学の範囲では、これまで習ってきたことや、これから習うことにド・モルガンの法則が大きくは関係しないのだが、 この法則は特に難しいことではないので、ここでは証明と覚え方を紹介する。

証明

まずは式(1)から証明する。

式(1)の右辺は下の図1のように表される。

\( \overline{A\cup B} \)は全体集合\( U \)の部分集合である\( A \)と\( B \)の和集合であるので、 灰色部分が右辺で表されている部分である。

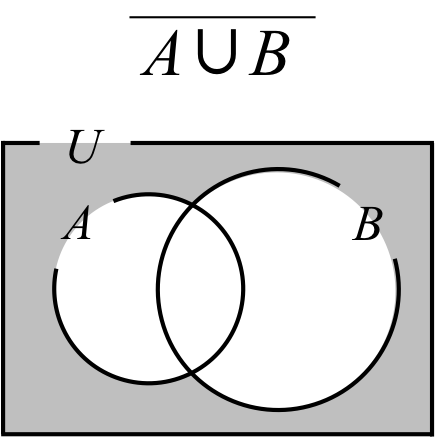
図1.

それでは、左辺について考えていこうと思う。

集合\( A \)の補集合\( \overline{A} \)と集合\( B \)の補集合\( \overline{B} \)は図2の1と2で表される。

\( \overline{A} \cap \overline{B} \)は\( A \)の補集合と\( B \)の補集合の和集合であるので、図2.の灰色の部分がその部分に当たる。

図1.と図2.を比較することで、式(1)が成り立つことがわかるだろう。

このようにして、図を書くことで、ド・モルガンの定理は簡単に証明することができる。

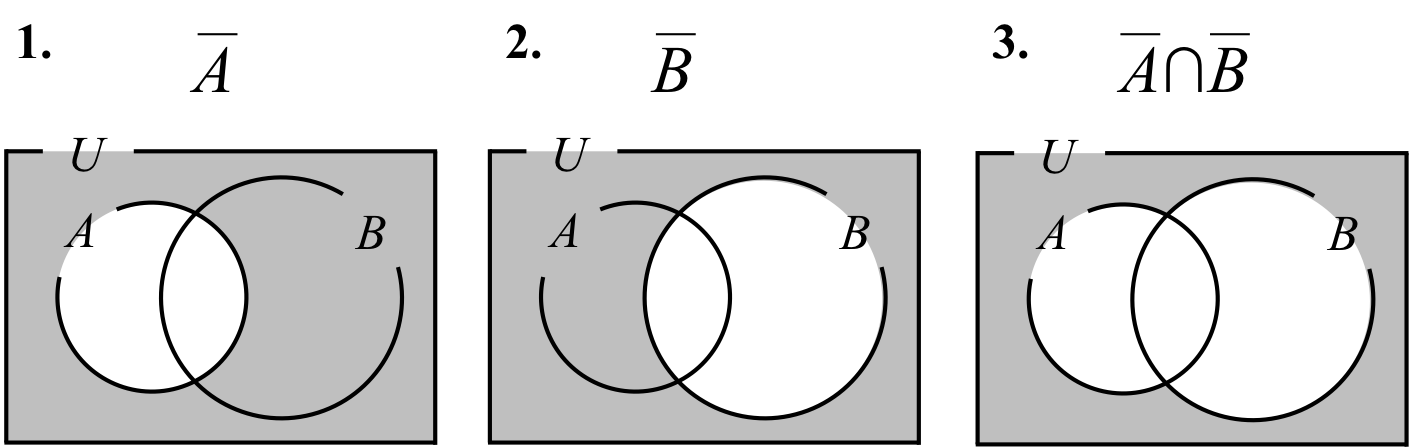
図2.

では次に、式(2)を証明しようと思う。

式(2)の右辺\( \overline{A\cap B} \)は集合\( A \)と\( B \)の共通部分の補集合である。

図で表すと図3.の灰色の部分になる。

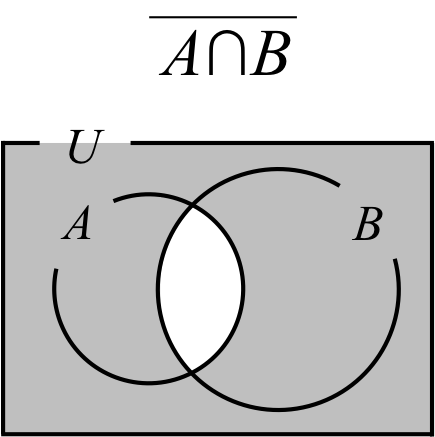
図3.

集合\( A \)と集合\( B \)の補集合は、図2.の時と同じように、図4.の1と2で表される。

このことから、\( A \)と\( B \)の補集合の共通部分は、図4の3の灰色の部分で表される。

つまり、図3と一致し、この法則も証明することができるのである。

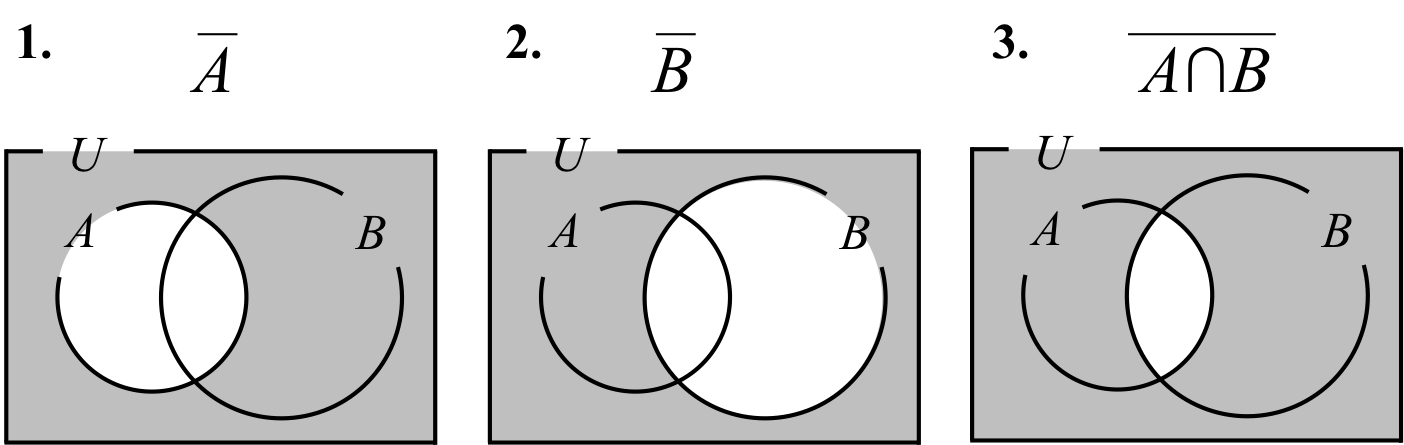
図4.

覚え方

数学で公式を覚えると言うのは邪道だとは思うのだが、ド・モルガンの法則は数学の中でも特に覚えておいた方が良いと思う法則である。

覚え方は実に簡単で図5のようになる。

\( A \)と\( B \)には補集合を表すバーがかかっている。

このバーを閉めようとすると、共通集合、和集合を表す\( \cap \)、\( \cup \)がひっくり返る。

これは式(1)、(2)どちらの場合でも有効である。

このことから、「バーを閉めようとすると、カップ（キャップ）がひっくり返る」と覚えていた。

なんだか怖い話のような覚え方だが、酒場（バー）を閉店させようとすると、そこにあったカップがひっくり返ってしまうと言う怪奇現象を想像して覚えておけば忘れることはないと思う。

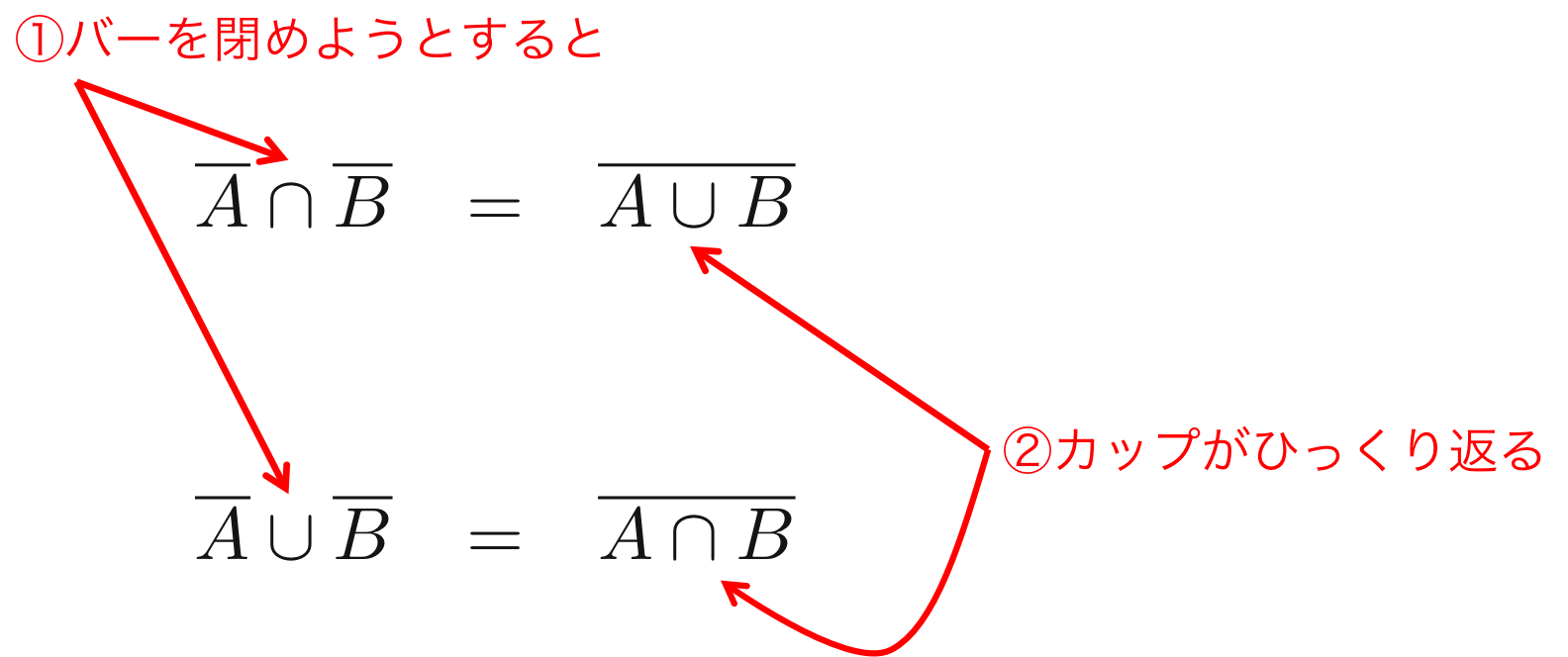
図5. ド・モルガンの法則の覚え方