補集合

カテゴリー：数学A

数学の問題では、まず集合\( U \)を決めて、要素としては\( U\)の要素を、集合としては\( U \)の部分集合\( A \)を考える場合が多い。

この時、\( U \)を全体集合と呼ぶ。

また、全体集合の部分集合\( A \)の要素ではないものを、集合\( A \)の補集合と呼び以下のように表される。

\begin{eqnarray} \bar{A} \end{eqnarray}

補集合\( \bar{A} \)と、全体集合\( U\)、部分集合\( A \)との関係を図にすると図1のようになる。

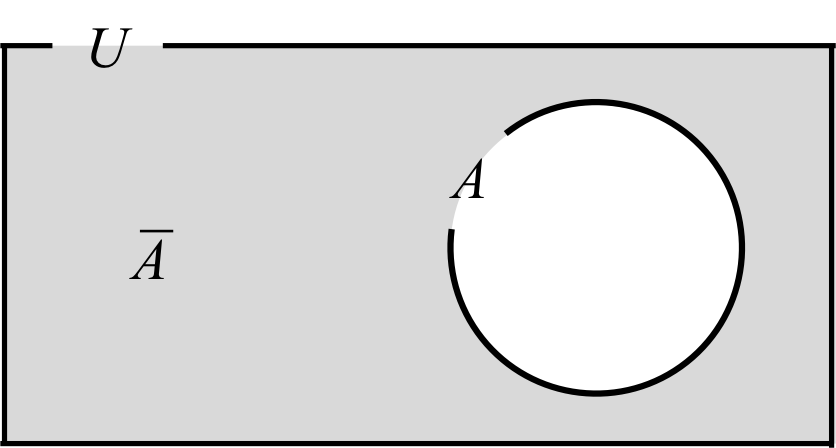
図1. 集合\( U \)とその部分集合\( A \)。\( A \)の補集合\( \bar{A} \)。

これだけでもだいたいわかると思うが、例を示してみる。

「20以下の自然数」という全体集合\( U \)があり、その中に「2の倍数」という部分集合\( A \)があった場合、\( A \)の補集合は

\begin{eqnarray} \bar{A} = \left\{ 1,\ 3,\ 5,\ 7,\ 9,\ 11,\ 13,\ 15,\ 17,\ 19 \right\} \end{eqnarray}

となるのである。

ちなみに補集合\( A \)の要素が\( x \)であったとすると、

\(x \in U \) 　　　　かつ　　　 \( x \notin A \)

である。この考え方はこれから出てくる集合の問題を解く上で最も基本的な点なので、よく理解しておくと良い。

また、空集合の補集合は全体集合、全体集合の補集合は空集合である。

つまり、

\(\bar{\varnothing} = U \) 　　　　かつ　　　 \( \varnothing = \bar{U} \)

ということである。

これは、全体集合以外の要素は考えないので、「全体集合の要素以外の要素はない（空集合になる）」。

「空集合以外の要素は全体集合の要素である」ということを意味しているのである。