共通部分と和集合
カテゴリー:数学A
集合\( A \)の要素が集合\( B \)の要素でもあるとき、集合\( A \)を集合\( B \)の部分集合と呼ぶ。
もし、集合\( A \)の要素の全てではなく、一部のみが集合\( B \)の要素であった場合はどうなるのであろうか?
この時、お互いに共通する要素のことを共通部分と呼ぶ。
共通部分を図で表すと、図1のようになる。図1のグレーの集合\( A \)と集合\( B \)の共通部分は以下のように表される。
\begin{eqnarray} A \cap B \end{eqnarray}
この式の読み方は「\( A \)と\( B \)の共通部分」または、「AキャップB」と呼ばれる。
キャップ(Cap)とは帽子のことで、記号\( \cap \)が帽子に似ていることに由来するのである。
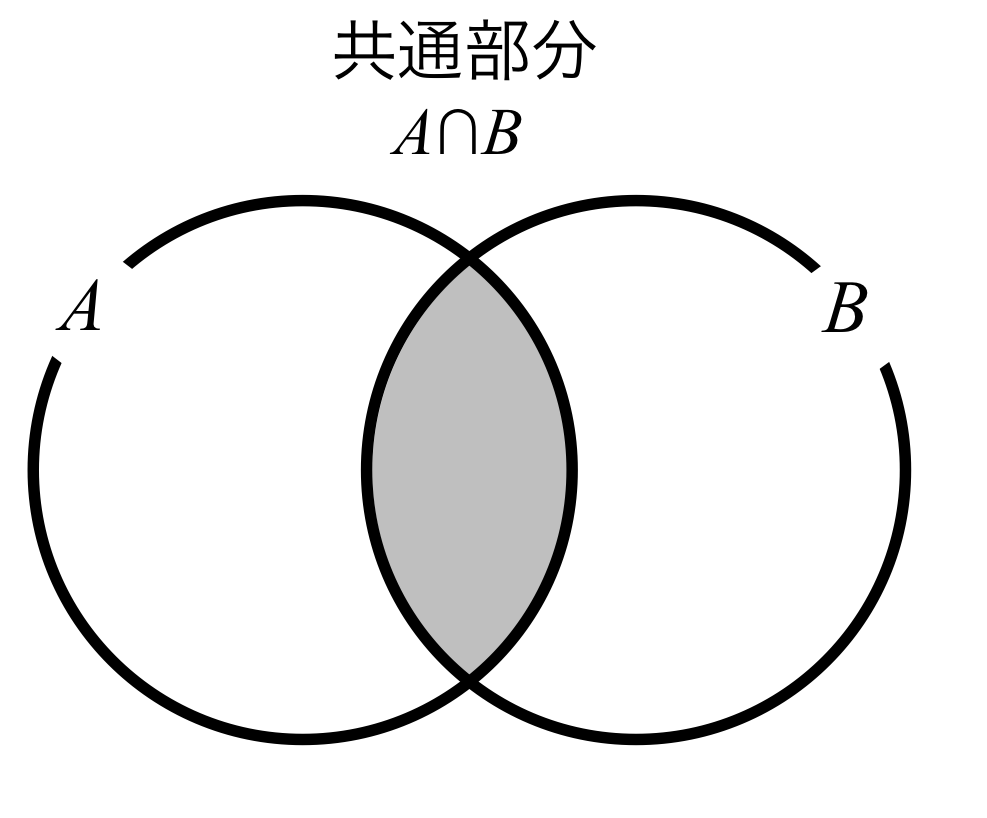
図1. 集合\( A \)と集合\( B \)の共通部分
共通部分だけでなく、集合\( A \)の要素と集合\( B \)の要素の両方を合わせた集合を和集合と呼ぶ。
集合\( A \)と集合\( B \)の和集合は以下のように表される。
\begin{eqnarray} A \cup B \end{eqnarray}
この読み方は、「\( A \)と\( B\)の和集合」または、「AカップB」と呼ばれる。
カップとはそのまま、マグカップとかコーヒーカップのカップである。
和集合を図で表すと、図2のようになり、集合\( A\)と集合\( B \)の要素が全て含まれていることがわかる。
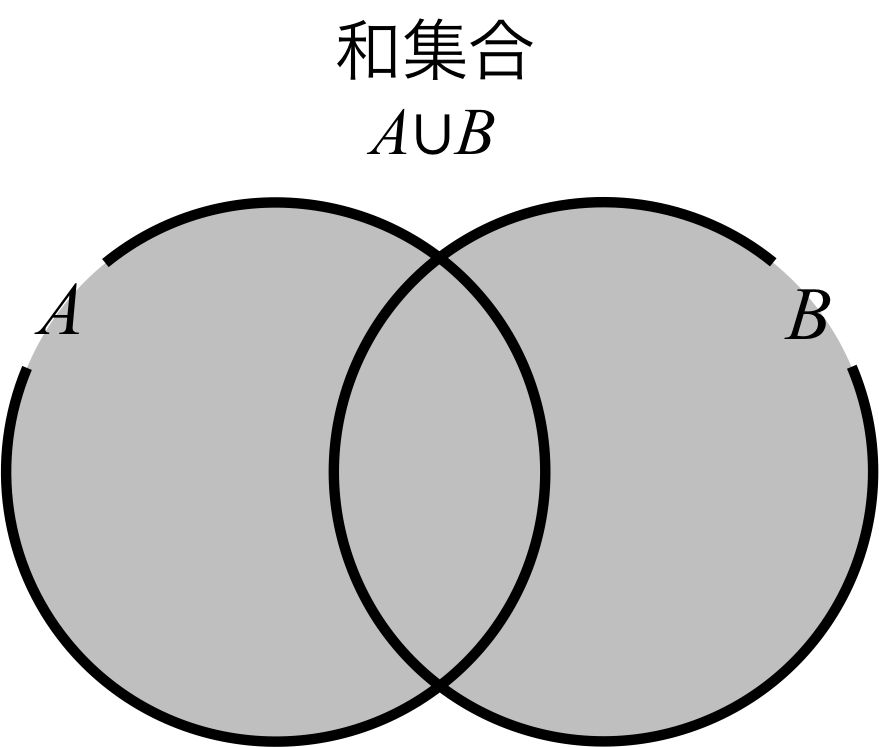
図2. 集合\( A \)と集合\( B \)の和集合
キャップとカップの覚え方
どちらが共通部分を示し、どちらが和集合を示すのかわからなくなることがある。
数学を覚えることは邪道であるが、この記号はどうしても覚えなくてはならない。
しかし、今のところ私はキャップとカップの覚え方に良い語呂合わせは思いつかない。
良い語呂合わせはないが、簡単な考え方ならある。
「カップにはたくさんの水を入れることができる。だから多くの要素を含む意味でカップ\( \cup \)で表される。反対にキャップは水を含めてもすぐに布から抜けて出て行ってしまうので、多くの水は貯められない。つまり、和集合より要素が少ない共通部分はキャップ\( \cap \)で表される。」
覚えにくいことに変わりはないのだが、上の概念を少しでも覚えておけばしばらくの間は忘れることはないと思う。
共通部分と和集合の具体例
では共通部分と和集合の具体例を示そう。
集合\( A \)は「12以下の3の倍数」、集合\( B \)は「12以下の2の倍数」であったとする。
この時、それぞれの集合の要素は、
\begin{eqnarray} A &=& \left\{ 3,\ 6,\ 9,\ 12 \right\} \\ B &=& \left\{ 2,\ 4,\ 6,\ 8,\ 10,\ 12\right\} \end{eqnarray}
であるので、共通部分は
\begin{eqnarray} A \cap B = \left\{ 6,\ 12\right\} \end{eqnarray}
である。
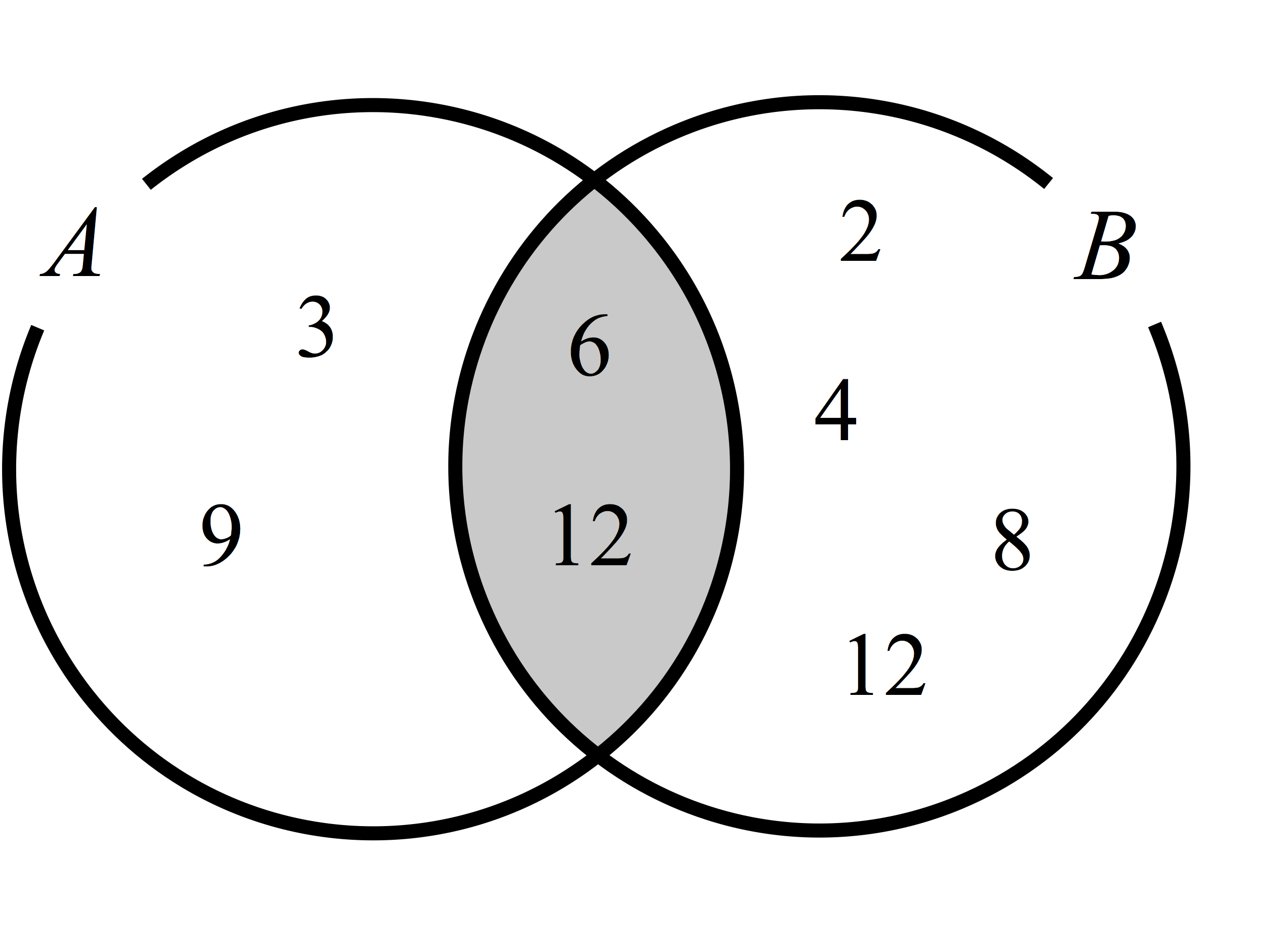
図3. 3の倍数の集合\( A \)と2の倍数の集合\( B \)の共通部分
次に和集合
\begin{eqnarray} A \cup B = \left\{ 2,\ 3,\ 4,\ 6,\ 8,\ 9,\ 10,\ 12\right\} \end{eqnarray}
と求めることができるのである。
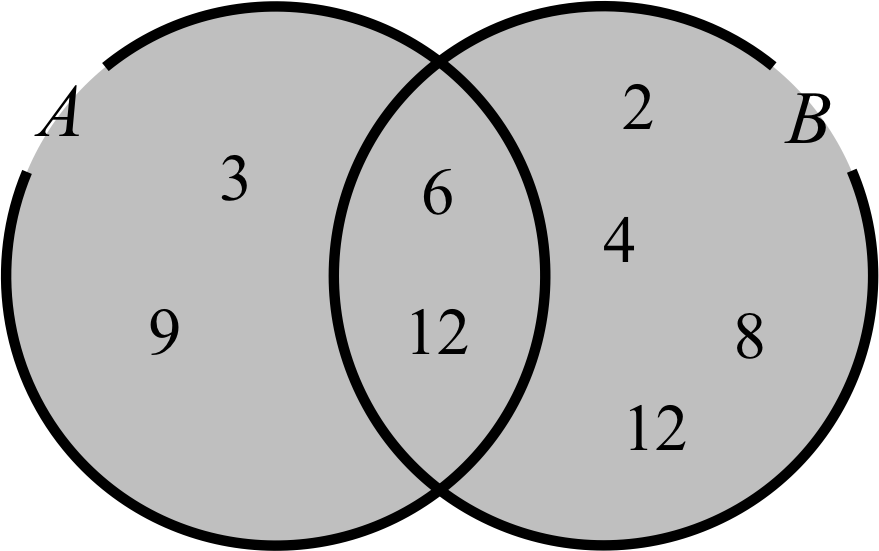
図4. 3の倍数の集合\( A \)と2の倍数の集合\( B \)の和集合
尚、集合\( A \)と集合\( B \)に全くの共通部分がない時、\( A \cap B \)は空集合であると言う。
これは、空集合で詳しく述べる。