全反射

カテゴリー：実験物理学

図1のように媒質Aから媒質Bに光が入射する場合を考える。

このとき、媒質Aの屈折率\( n_A \)は、媒質Bの屈折率\( n_B \)よりも大きい場合を考える（\( n_A > n_B\)）。

直感的に考えると、媒質Aが水で媒質Bが空気を想定してもらうとわかりやすいと思う。（水槽を上から見ているイメージ）

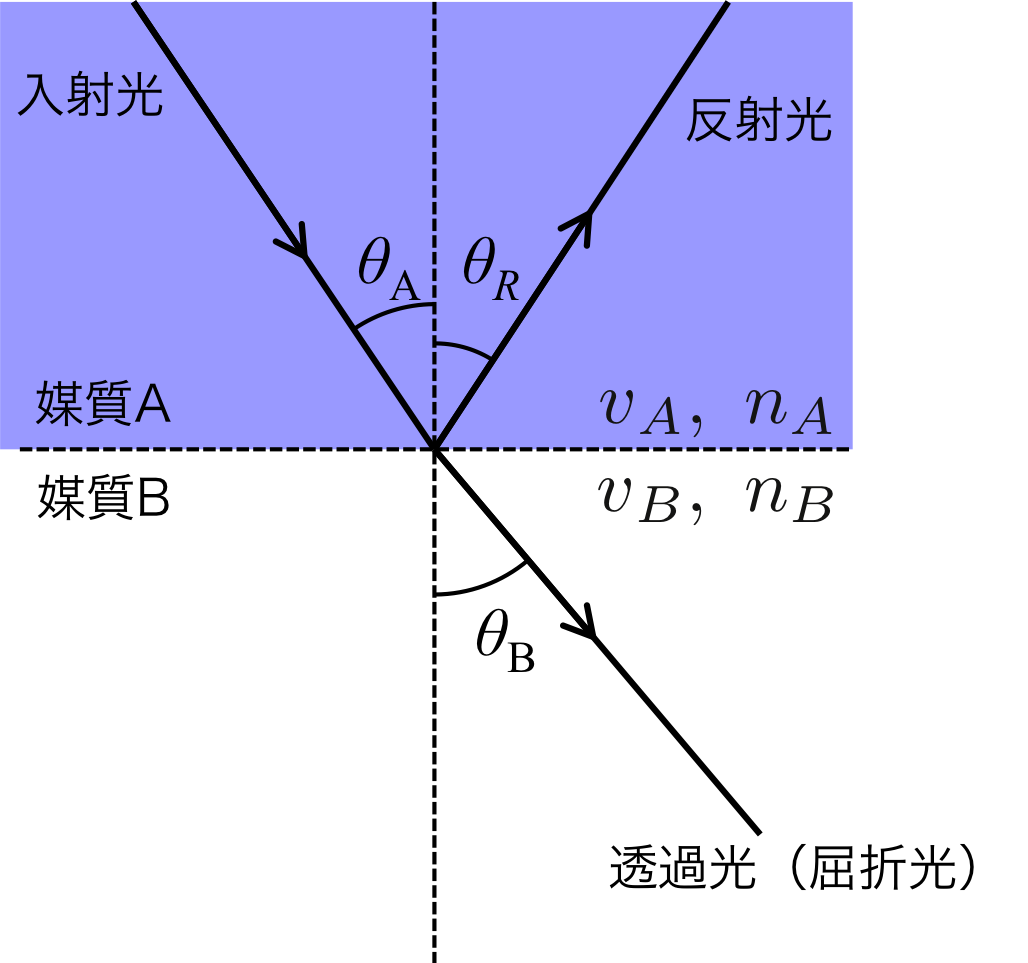
図1. 入射光の反射と屈折

ここで、入射角と屈折角の関係は、スネルの法則を使って、

\begin{eqnarray} n_A \sin \theta_A = n_B \sin \theta_B = 一定\ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

と表すことができるのである。

この時、入射光はすべて透過光として、媒質Bに侵入するのではなく、その一部は反射光として、媒質Aと媒質Bの境界面で反射される。

尚、入射角\( \theta_A \)と反射角\( \theta_R \)は等しくなる。

式(1)からわかるように、入射角\( \theta_A \)をどんどん大きくしていくと、同じように屈折角\( \theta_B \)も大きくなっていく。

やがて、図2に示すように、屈折角\( \theta_B \)は90度（直角）になってしまう。

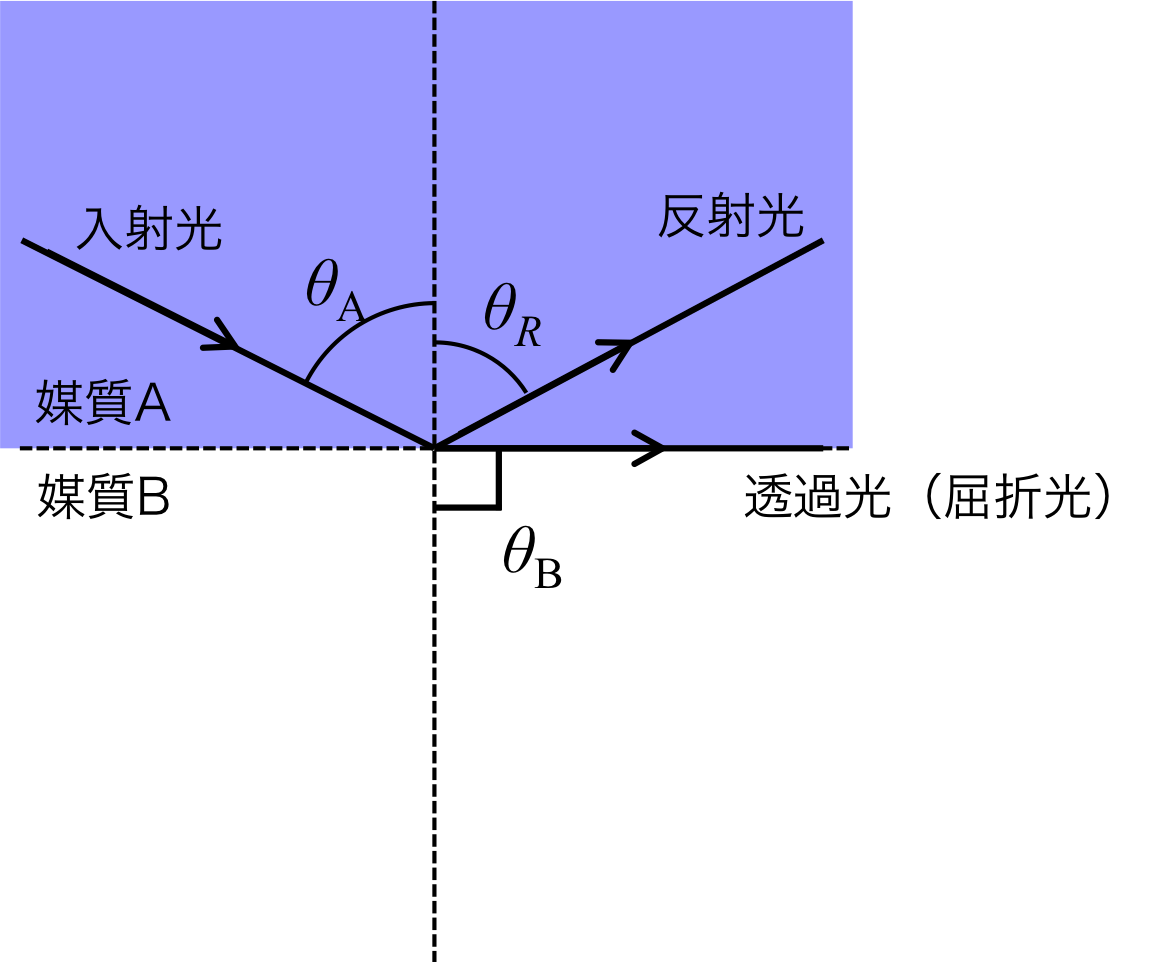
図2. 入射角を臨界角まで大きくした場合

直角になっても尚、入射角を大きくした場合はどうなるであろうか？

当然、屈折角は90度より大きくすることはできないので、媒質Bに光は侵入することができなくなる。

そうなると、入射光のすべては反射光となる。つまり、すべて反射されるのである。

これを全反射という。

屈折角が90度になる入射角のことを臨界角\( \theta_m\)と呼び、スネルの法則である式(1)から以下のように表される。

\begin{eqnarray} \sin \theta_m = \frac{\sin \theta_m}{\sin 90^\circ} = \frac{n_B}{n_A} \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

である。臨界角より大きな入射角で媒質Bに入射する場合は、全反射が起きるのである。