光学的深さ
カテゴリー:実験物理学
波長の光が大気を通り抜ける時に、どの程度弱められてしまうのか?ということを表現するために光学的深さが用いられる。
「光学的厚さ」と「光学的深さ」を同一のものとして説明していることもあるが、厳密には異なる。
このページでは光学的深さについて説明した後に、光学的深さと光学的厚さの違いについて簡単に述べる。
また、ここでは大気における光学的深さについて説明する。
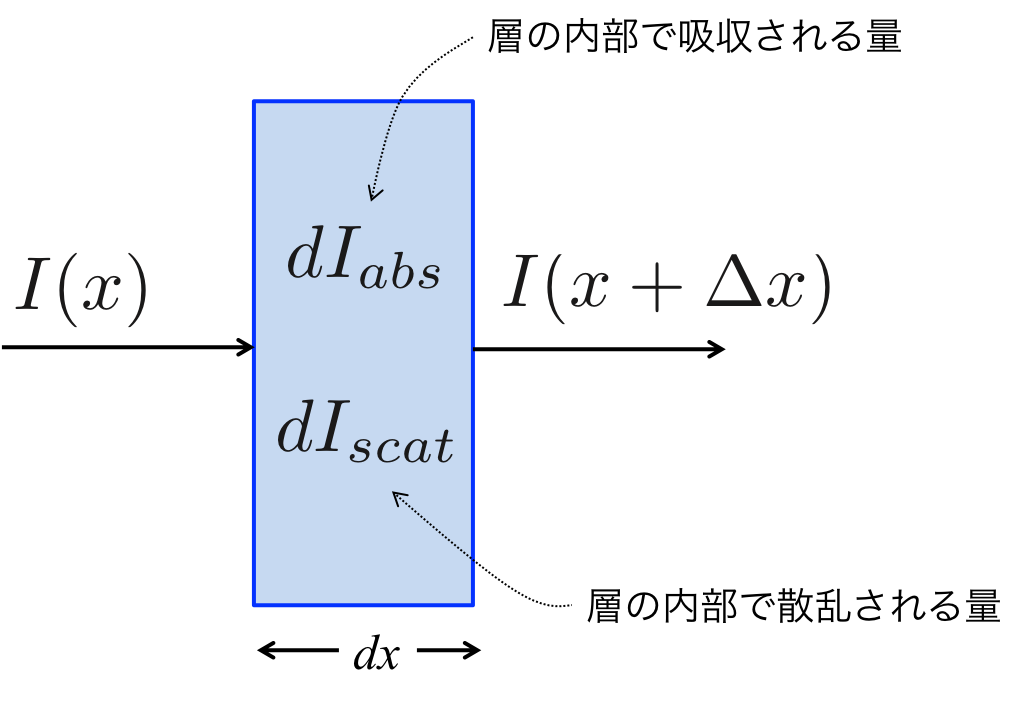
図1. 薄い層を通過する光(電磁波)
図1のように幅\( dx \)の薄い層に強度\( I(x) \)の光(電磁波)が入射する場合を考える。
この層では光が散乱と吸収によって\( dI_{scat}\)、\( dI_{abs}\)だけ弱められる。
すると、層から出た光の強度\( I(x+dx) \)は以下のように表すことができる。
\begin{eqnarray} I(x+dx) = I(x) - dI_{abs} - dI_{scat} \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
ここで、\( dI_{abs} \)と\( dI_{scat} \)は層の中にある大気の数密度\( n \)に比例すると考えられている。
従って、大気の固有な性質である吸収断面積\( \sigma_{abs} \)と散乱断面積\( \sigma_{scat} \)を使うことで、
\begin{eqnarray} dI_{abs} &=& n \sigma_{abs} I(x) dx \ \ \ \ \ \ \ \ \ \ \ \ (2) \\ dI_{scat} &=& n \sigma_{scat} I(x) dx \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
と表すことができる。
ここで、吸収断面積と散乱断面積については詳しくは説明しないが、その次元は\( \mathrm{m}^2 \mathrm{molecule}^{-1} \)である。
式(2)、式(3)を式(1)に代入すると、
\begin{eqnarray} dI = - dI_{abs} - dI_{scat} = I(x-dx) - I(x) = - n (\sigma_{abs} + \sigma_{scat}) I(x) dx \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
となる。これを変形分離すると、
\begin{eqnarray} \frac{dI}{dx} = - n (\sigma_{abs} + \sigma_{scat}) I(x) \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
となり、これを積分するとことで、
\begin{eqnarray} I(x) = I_0 \exp \left\{ - n (\sigma_{abs} + \sigma_{scat} ) x \right\}\ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
を得る。このようにある層に入射した光は、吸収と散乱を受けて指数関数的に減少するのである。
ここで、
\begin{eqnarray} \tau = - n (\sigma_{abs} + \sigma_{scat} ) x = \frac{\ln I_0}{\ln I(x)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
が光学的深さと定義されているのである。
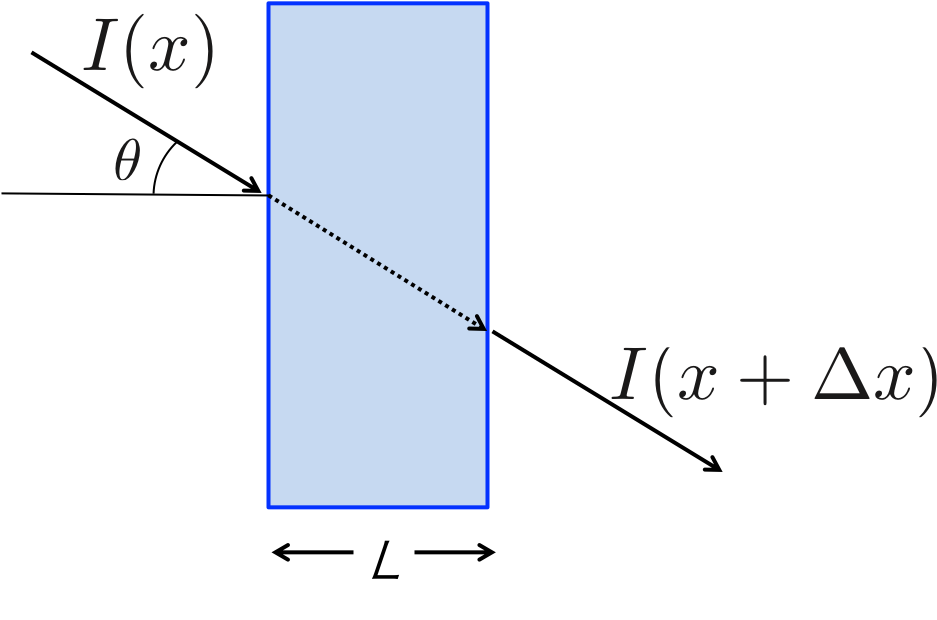
図2. 斜めに薄い層を通過する光(電磁波)
光学的深さと光学的厚さの違い
以上で説明したものが光学的深さである。
では光学的厚みとはなんだろうか?上で説明した光学的深さとは、層に対して垂直に侵入した場合のことである。
「光学的厚み」とは任意の光路での「光学的深さ」のことを意味する。
つまり、図2のように斜めに光が入射した場合は、層の内部の距離は\( L /\cos \theta \)となり、 光学的厚みは\( \tau / \cos \theta \)となるのである。
ここで、\( \tau = - n (\sigma_{abs} + \sigma_{scat} ) L \)である。
斜めに入射した場合は当たり前ではあるが、層内で長い距離を伝搬しなくてはならないので、減衰も大きくなる。