F値
カテゴリー:実験物理学
F値(Fナンバー)とは、レンズの焦点距離をレンズの有効口径で割った値である。
主に用いられるのはカメラで、そのレンズの明るさを測るのに用いられる。
もちろんレンズの有効口径が大きければ大きいほどたくさんの光を集めることができるので、F値が小さいレンズほど明るい像になる結像レンズと言える。
このページではより詳しくF値について説明しようと思う。
図1に凸レンズの場合の焦点距離と有効口径の関係を示す。
通常焦点距離は、レンズの主点から、そのレンズの焦点までの距離のことを言う。 今は凸レンズ1枚しか考えていないので、主点は凸レンズの中心になる。
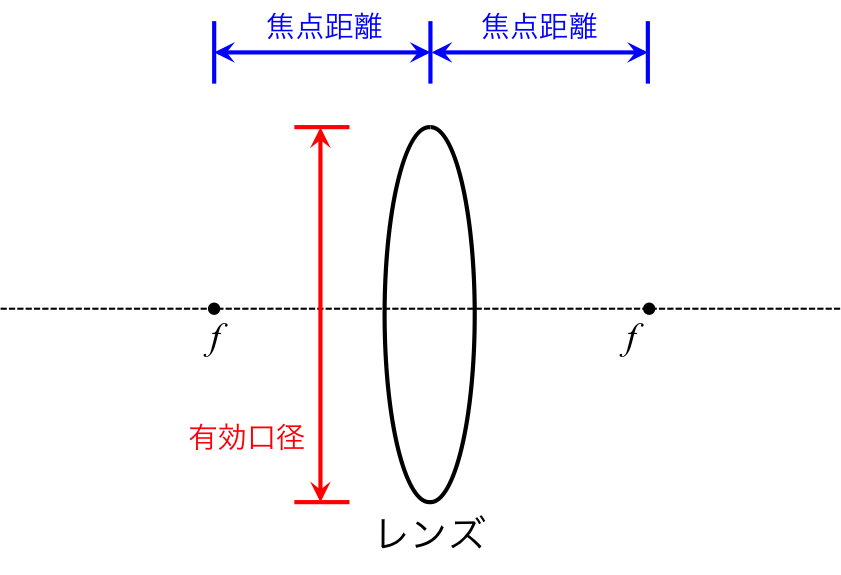
図1. レンズの焦点距離と有効口径
では、焦点距離を\( f \)、有効口径を\( \Phi \)として、F値を\( f_n \)とすると、
\begin{eqnarray} f_n = \frac{f}{\Phi}\ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
となる。もし、レンズの光を集められる面積が2倍になったならば、レンズを通過する光も2倍になる。
反対に、もし、光を集められる面積が半分になったならば、レンズを通過する光は1/2になる。
こういった場合にF値がどのように変化するのか見てみよう。
光を集められる面積(光を受ける面の面積)\( S \)は
\begin{eqnarray} S = \frac{1}{4} \Phi^2 \pi \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
となる。ここで、\( \Phi \)が\( \Phi' \)に変化して、光を集められる面積が半分になったとしよう。
すると、
\begin{eqnarray} \frac{1}{2} S = \frac{1}{8} \Phi^2 \pi = \frac{1}{4} \Phi'^2 \pi\ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
となり、\( \Phi' = \frac{1}{\sqrt{2}} \Phi \)の関係が導ける。
つまり、光を集められる面積が半分になると、有効口径は\( 1/\sqrt{2} \)になるのである。
言い換えると、光を集められる面積が半分になるとF値は\( \sqrt{2} \)倍になる。
逆に、光を集められる面積が2倍になると、F値は\( 1/\sqrt{2} \)倍になるのである。
カメラなどではよくF値を変えながら撮影する。
ここでは詳しく原理を説明しないが、F値が小さいほどシャッタースピードは早くなり、背景がボケる写真を撮ることができる。
逆にF値が大きい設定にすれば背景はボケないためピンボケしにくい写真を撮ることができる。
しかし、上で説明したようにF値を変えるには有効口径を変化させないといけない。
レンズはほとんど伸び縮みしないので、その場でレンズの有効口径を変えることはできない。

図2. カメラのレンズと絞り
そこでカメラでは図2で示すように絞りというもので、レンズの端から光が入らないようにする。
こうすることで、レンズの実質的な直径を小さくすることができる。 ”有効”とはこういう意味なのである。
絞りを絞るほど、有効口径を小さくすることができて、F値を大きくすることができる。
逆に背景をぼかした写真を撮りたい場合は、絞りを限界まで開けるのである。
通常、市販されているレンズのカタログに書いてあるF値は、この絞りを全開にした場合のF値が示されており、開放F値と呼ばれる。
開放F値はそのカメラのレンズが設定できる最も小さいF値である。