>レンズの公式(凹レンズ)
カテゴリー:実験物理学
凹レンズは図1のように正立の虚像を作るのである。
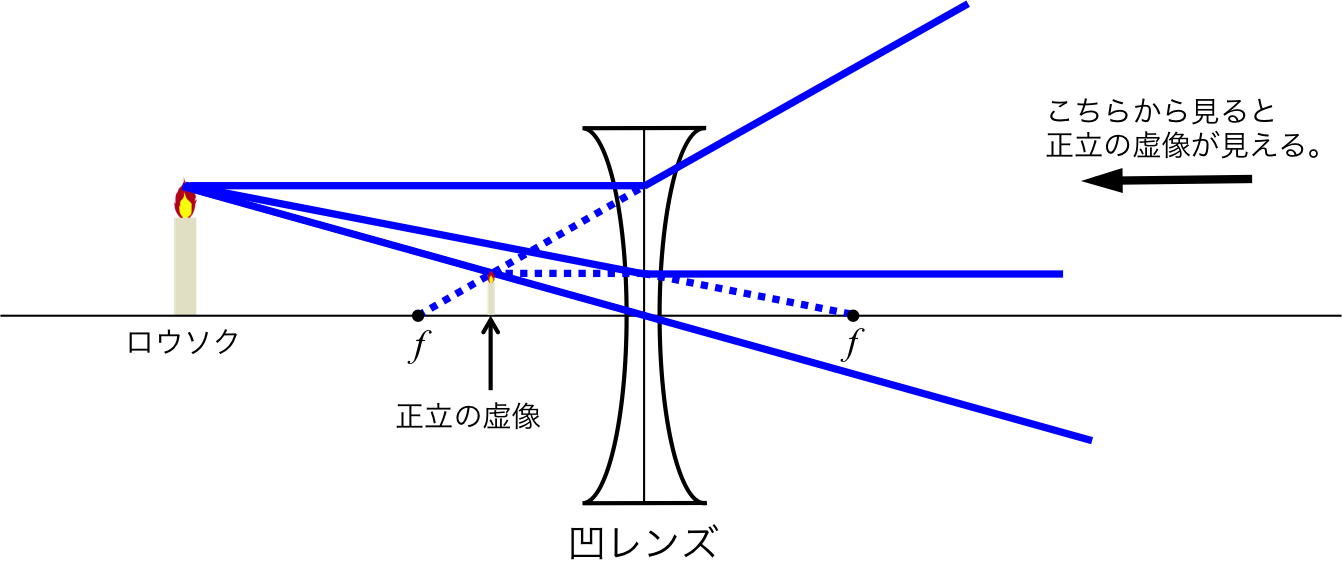
図1. 凹レンズが作る像
ロウソクなどの物体を置いたときに、どこにどれほどの大きさの正立の虚像が作られるかはレンズの公式に従う。
基本的には凸レンズのレンズの公式と同じ導出方法で凹レンズのレンズの公式を導くことができる。
レンズの中心から物体を置いた位置までの距離を\( a \)とし、正立の虚像が作られる位置を\( b \)とする。
また、レンズの中心から焦点までの距離を\( F \)とする。
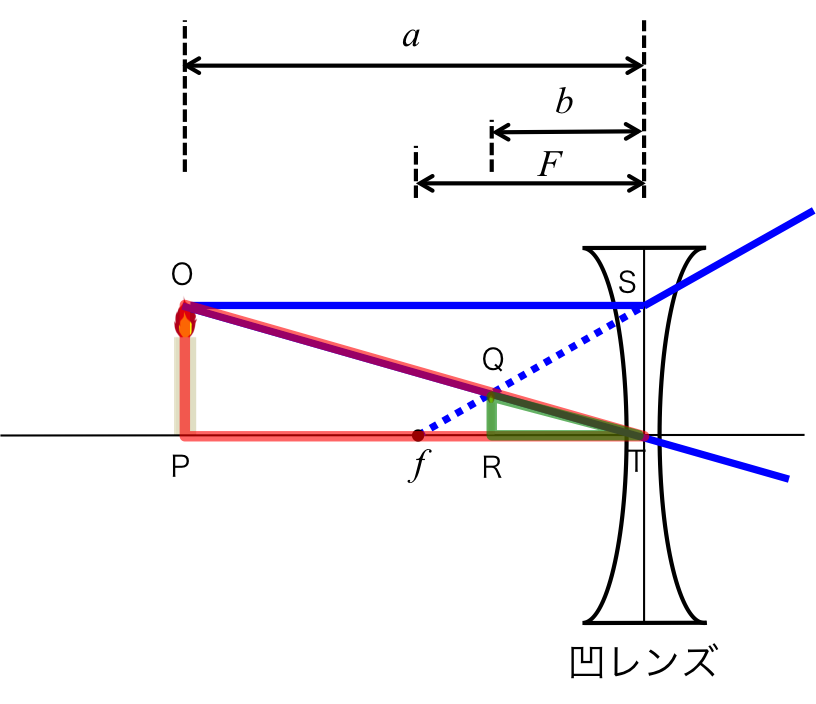
図2a.
図2aに示すように、\( \triangle{OPT} \)と\( \triangle{QRT} \)は相似形であるので、
\begin{eqnarray} OP : QR = a : b \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
の関係を導ける。
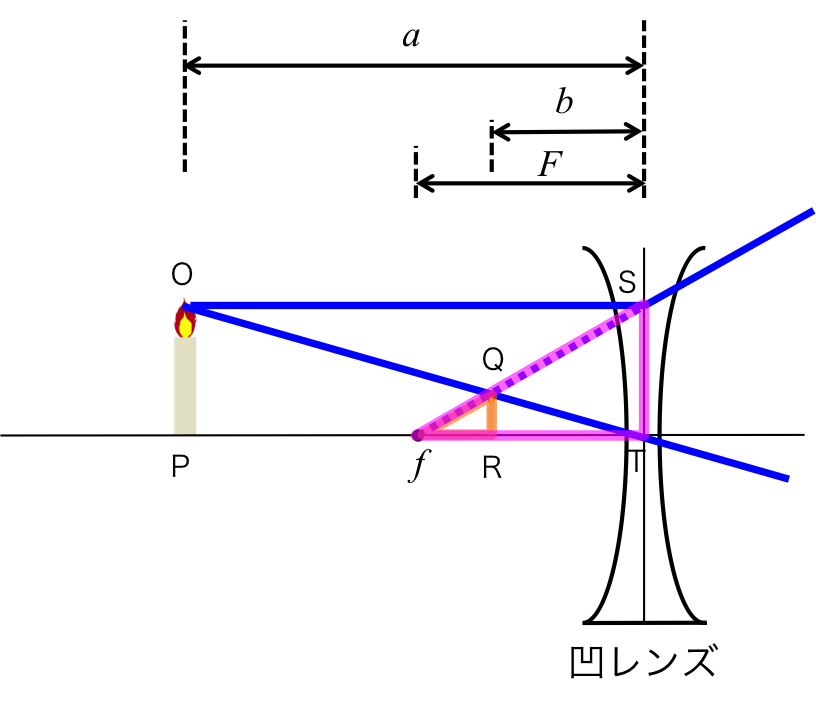
図2b.
次に図2bに示すように、\( \triangle{STF} \)と\( \triangle{QRF} \)は相似形であるので、
\begin{eqnarray} ST : QR = F : F-b \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
である。
式(1)と式(2)から、\( OP=ST \)であることを使って、
\begin{eqnarray} \frac{1}{a} - \frac{1}{b} = - \frac{1}{F} \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
と導ける。
この式(3)が凹レンズにおけるレンズの公式である。
また、倍率\( m \)は式(1)から
\begin{eqnarray} m = \frac{QR}{OP} = \frac{b}{a} \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
で表されるのである。
凸レンズの場合は物体を置く位置で1を超えたり下回ったりして、倍率が変化したが、凹レンズの場合、どのような場合でも倍率が1を超えない。
スポンサーリンク