クーロンの法則のベクトル表記
カテゴリー:電磁気学
クーロン力は向きと大きさを持つので、ベクトル表記をすることができる。 クーロンの法則で示されたものは、 \begin{eqnarray} F = \frac{1}{4\pi\epsilon_0} \frac{Q_1 Q_2}{r}\ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} である。この時、\( r \)は2つの物体間の距離である。式(1)で示されるクーロン力は大きさは示されているので、向きを与えればいいわけである。
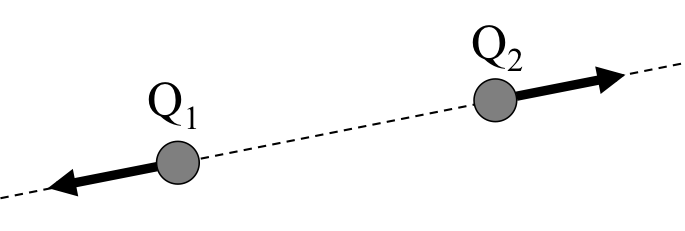
図1 符号が同じ電荷に帯電した物体
図1では、クーロン力はどの方向にかかるのかを示した。2つの帯電体しかない場合は、2つの帯電体を結んだ直線上にクーロン力がかかる。 2つの帯電体の電荷の符号が同じ場合は、引き離す向きに、符号が異なる場合は引き合う向きにクーロン力はかかる。 つまり、電荷\( Q_1 \)と\( Q_2 \)に帯電した物体を置き、そこにかかる力を示すと図2のようになる。
この図1の黒い矢印のクーロン力をベクトルで表記する。
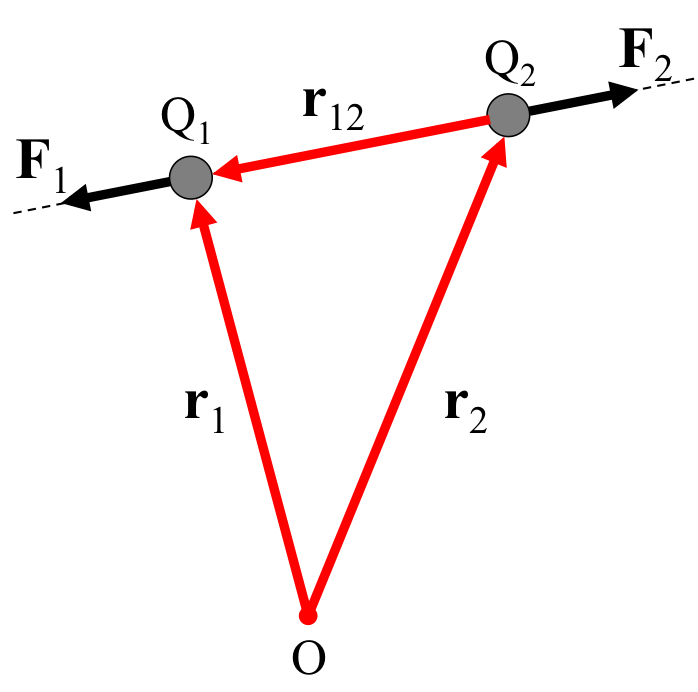
図2 帯電した物体の位置ベクトルとクーロン力のベクトル
そのためには、まず図2のように\( Q_1 \)に帯電した物体と\( Q_2 \)に帯電した物体の位置ベクトル\( {\bf r}_1,\ {\bf r}_2 \)から、2つの帯電体を結んだ直線と同じ向きの(\(Q_2\)から\(Q_1\)へ向かう)ベクトル、\( {\bf r}_{12} \)を求める。 この時、原点を\( O \)とした。 図2から\( {\bf r}_{12} \)は \begin{equation} {\bf r}_{12} = {\bf r}_1 - {\bf r}_2\ \ \ \ \ \ \ \ \ \ (2) \end{equation} と示される。
このベクトルを\(Q_1\)に帯電した物体が加えられるクーロン力である\(F_1\)に掛けてやれば\(F_1\)に向きを与えることができる。 しかし、\( {\bf r}_{12} \)は大きさを持ってしまっているので、このまま掛けるとクーロン力の大きさが変わってしまう。 そこで、\( {\bf r}_{12} \)と向きが同じであるが、大きさ1で掛け合わせた時に、相手側の大きさを変えることなく、向きだけを与えることができるベクトルである\( {\bf r}_{12} \)方向の単位ベクトルを掛けてやればいいのである。 単位ベクトルにするためには、そのベクトルの大きさでベクトルを割ってやればいいのである。 つまり、\( {\bf r}_{12} \)ベクトルの単位ベクトル\( {\bf \hat{r}}_{12} \)は、 \begin{eqnarray} {\bf \hat{r}}_{12} &=& \frac{{\bf r}_{12}}{\left| {\bf r}_{12} \right|} &=& \frac{{\bf r}_1 - {\bf r}_2}{\left| {\bf r}_1 - {\bf r}_2 \right|} \ \ \ \ \ \ \ \ (3) \end{eqnarray} となる。これを、式(1)に掛け合わせることで、クーロン力をベクトル表記することができる。 \begin{eqnarray} {\bf F}_1 &=& \frac{1}{4 \pi \epsilon_0}\frac{Q_1 Q_2}{r_{12}^2} {\bf \hat{r}}_{12} \\ \\ &=& \frac{1}{4 \pi \epsilon_0} \frac{Q_1 Q_2}{\left| {\bf r}_1 - {\bf r}_2 \right|^2} \frac{{\bf r}_1 - {\bf r}_2}{\left| {\bf r}_1 - {\bf r}_2 \right|} \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} ちなみに、\( Q_2 \)に帯電した物体にかかるクーロン力は、単位ベクトル\( {\bf \hat{r}}_{12} \)を反対向きにしてやればいいわけで、 それは、式(2)のベクトル\( {\bf r}_1 \)と\( {\bf r}_2 \)の引き算を入れ替えてやればいいのである。 つまり、\( Q_2 \)に帯電した物体にかかるクーロン力\( {\bf F}_2 \)は \begin{equation} {\bf F}_2 = \frac{1}{4 \pi \epsilon_0} \frac{Q_1 Q_2}{\left| {\bf r}_2 - {\bf r}_1 \right|^2} \frac{{\bf r}_2 - {\bf r}_1}{\left| {\bf r}_2 - {\bf r}_1 \right|} \ \ \ \ \ \ \ \ \ \ (5) \end{equation} と表されるのである。
最後に\( Q_1 \)に帯電した物体の座標を\( (x_1,\ y_1,\ z_1) \)、\( Q_2 \)に帯電した物体の座標を\( (x_2,\ y_2,\ z_2) \)とするとクーロン力の\(x\)方向、\(y\)方向、\(z\)方向の成分はどのように表されるか考えてみよう。 式(4)を変形して、 \begin{eqnarray} {\bf F}_1 = \frac{1}{4 \pi \epsilon_0}\frac{Q_1 Q_2}{r_{12}^2} {\bf \hat{r}}_{12} = F_1 \frac{{\bf r}_1 - {\bf r}_2}{\left| {\bf r}_1 - {\bf r}_2 \right|} \ \ \ \ \ \ \ \ (6) \end{eqnarray} であるので、各方向成分は \begin{align} F_{1x} &= F_1 \frac{x_1 - x_2}{\sqrt{ (x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2 }} &(7) \\ F_{1y} &= F_1 \frac{y_1 - y_2}{\sqrt{ (x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2 }} &(8) \\ F_{1z} &= F_1 \frac{z_1 - z_2}{\sqrt{ (x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2 }} &(9) \end{align} となる。つまり、帯電した2つの物体の座標と電荷がわかれば、その物体にかかるクーロン力の各方向成分はすぐ分かるのである。