クーロンの法則

カテゴリー：電磁気学

クーロンの法則とは、荷電粒子の間に働く力のことであり、その力が電荷の積に比例し、距離の2乗に反比例することを示した法則である。

正（プラス）と負（マイナス）の電荷があり、同じ種類の電荷であれば、お互いに引き離そうとし、異なる種類の電荷の場合は引き付け合う力が働くことが1700年代前半にはすでに知られていた。

この力にどのような特性があるのかは謎であったが、1700年代後半にフランスの物理学者シャルル・ド・クーロンが、この力がどのような特性で互いに影響を及ぼすのかを明らかにした。

1785年、クーロンは非常に感度の良いねじり天秤を使って２つの帯電した小さな球の間に働く力を測定し、それらに以下の法則があることに気づいた。

2つの帯電体の間に働く力は、2つの帯電体の持つ電荷の積に比例し、距離の2乗に反比例する。

この法則のことをクーロンの法則と呼び、2つの帯電体に働く力のことをクーロン力と呼ぶのである。

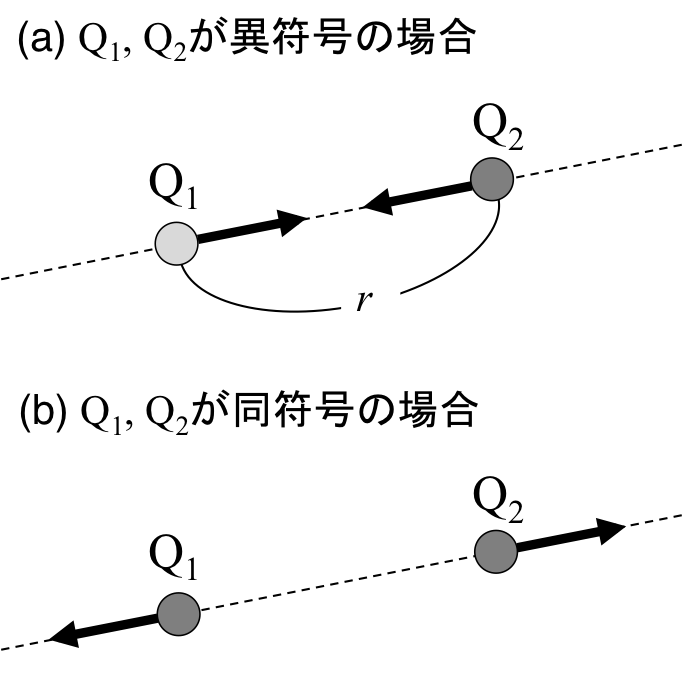
図1 それぞれの影響を及ぼし合う電荷（(a), (b)は十分離れており、影響を及ぼし合わないとする）

ではクーロンの法則を図1を使って簡単に説明しようと思う。

図1のように電荷\( Q_1 \)と電荷\(Q_2\)も持った物体が置かれている場合を考える。

\(Q_1\)と\(Q_2\)が異なる符号の電荷の場合、互いの物体は引かれあう。

\(Q_1\)と\(Q_2\)が同じ符号の場合、互いの物体は離れる向きにクーロン力がかかる。

この時、注意しなければならないのは、２つの物体にかかるクーロン力は等しいということである。

つまり、帯電体はもう一つの帯電体から力を受けているだけではなく、力を与えているという作用・反作用の法則がクーロンの法則の中でも成り立っているのである。

この力は２つの物体の距離\( r \)が小さければより強く、\( r \)が大きくなると急激に弱くなる。

つまり、ものすごく遠く引き離された物体は、お互いにほとんどクーロン力を受けないのである。

ではクーロン力を式で表してみる。

クーロンの法則は2つの帯電体の間に働く力は、2つの帯電体の持つ電荷の積に比例し、距離の2乗に反比例するので、これを式にすればよいので、 クーロン力を\( F \)、帯電体のそれぞれの電荷を\(Q_1\)、\(Q_2\)、2つの帯電体の距離を\( r \)とすると、

と表される。この時、\( 1/4\pi\epsilon_0 \)は比例定数で、

である。特に、\( \epsilon_0 \)は真空の誘電率と呼び、
\begin{eqnarray} \epsilon_0 = 8.854187817\cdots \times 10^{-12}\ \ \ \ \ \mathrm{C^2/N\cdot m^2}\ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

である。

式(1)で示されるような、クーロン力に似た力として、万有引力が有名である。

万有引力は、2つの物体の質量の積に比例し、距離に反比例するという力である。

一見似ているようではあるが、実は万有引力は引き合う力だけで、クーロン力のように引き離す力（斥力）は存在しないのである。

これは、物体の質量は正しかありえないが、電荷は負の場合もありえると言うことである。

このようにクーロン力の場合、電荷の正負に注意しながら力がかかる方向を考えなければいけないのである。

次のページでは、力のかかる向きをもっと分かりやすく示すために、クーロン力のベクトル表記について説明する。