電子の発見

カテゴリー：電磁気学

古くは物質の最小単位は、原子であると考えられていた。イギリスの科学者であるJ. J. トムソンは陰極線の実験により、原子には後に電子とわかる負の電荷を持った粒子が含まれていることを発見した。これは1897年のことである。ではここでは電子の発見について説明していく。

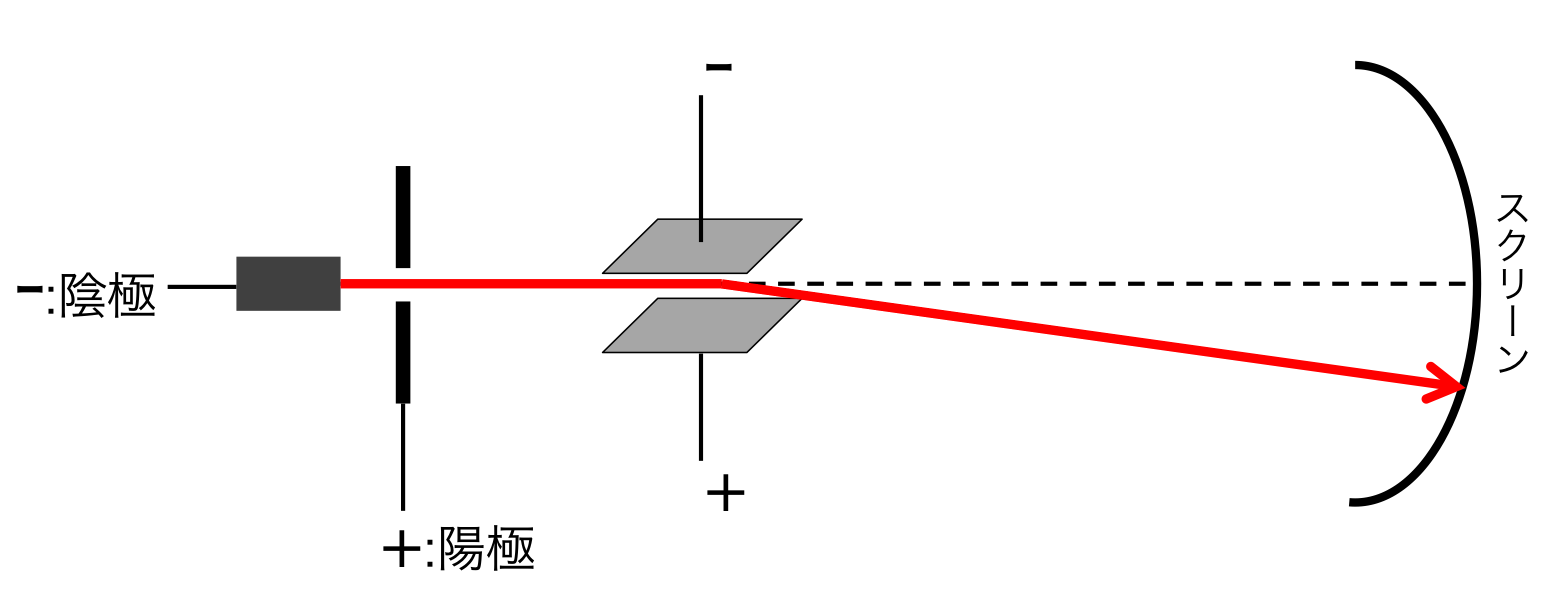
図1 真空中に電子を放出し、電極間を通過させる装置。電子はスクリーンに衝突すると白い跡を付ける。

図1がトムソンが電子を発見した実験装置である。左端の陰極と陽極の間に高電圧をかける。すると電子が、陰極から陽極に向かって飛び出す。陽極に図のようにスリット（隙間）を開けておくと、陰極から飛び出した電子の一部は右側に勢い良く飛び出す。このようにして電子のみを取り出す（これを電子ビームと呼ぶ）。この実験装置内部は真空になっており、電子は空気の分子と衝突することなく右に向かって進む。電子は電極板の間を通り、右端のスクリーンに到達する。スクリーンは電子が衝突すると、白く跡が残るようになっている。

まずは電極板に電圧をかけずに電子を射出すると、電子はまっすぐ飛び、点線上を運動してスクリーンに衝突する。この時、重力によって下向きに力を受けるが電子の速度が極めて早く、重力によって受ける力は無視できるほど小さい。次に、電極板に電圧をかけ、電場を発生させておく。帯電した物体が、電場によって力を受けることは知られているので、この時、もし電子の軌道が変えられたなら電子は電荷を持っているということになる。実際に観測を行うと、図1の赤線で示したように電子は下向きに曲げられてスクリーンに投影された。さらに電場は下から上に向かってかけられていたが、電子が下向きに軌道を変えられたことから、電子は負の電荷を持っていることがわかった。このようにして、トムソンは原子を構成するものの一つに電子と言う負の電荷を持った粒子が含まれていることを発見したのである。

トムソンは電子の性質を明らかにしようとした。電子の質量はどれくらいか？どれくらいの電荷を持っているのか？しかし、これらを明らかにすることはこの実験ではできなかったが、電荷と質量の比である比電荷を求めることに成功している。ちなみに比電荷は\( e / m_e \)と表され、\( e \)は電子の電荷（電気素量）、\( m_e \)は電子の質量である。トムソンはこの功績により1906年にノーベル物理学賞を受賞している。

では次に比電荷をトムソンはどうやって求めて行ったのかを説明していく。

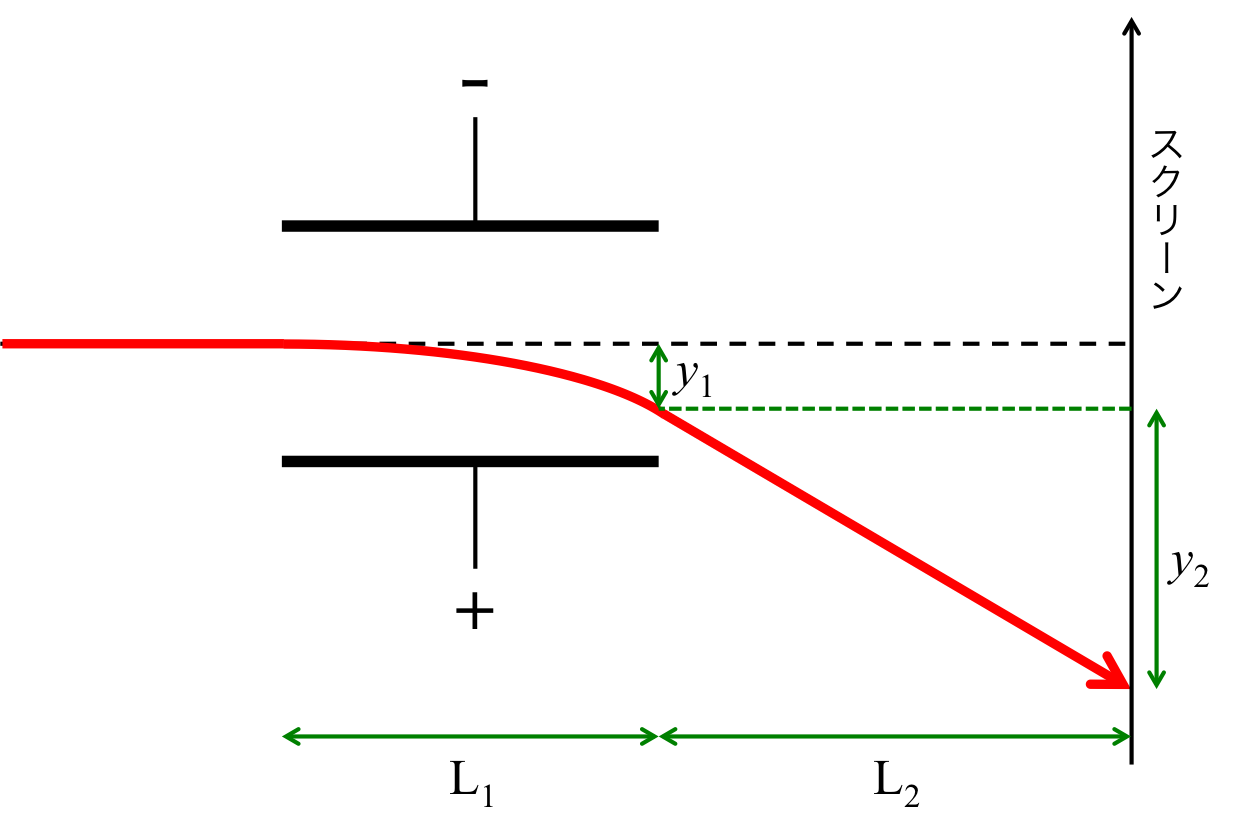
図2 トムソンの実験装置中を運動する電子の軌跡

図2にトムソンの実験の断面図を示した。電子は電極板の間のみで下向きに加速を受け、電極を脱出すると、直線でスクリーンへ向かう。ここで、電子の横方向（x方向）の速度を\( v_0 \)として、電極板の大きさを\( L_1 \)、電極板の端からスクリーンまでを\( L_2 \)とする。電極板の間に電子がいる間の運動方程式は

\begin{eqnarray} m_e a_y = - e E \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

となる。この時、\(a_y\)を\(y\)方向の加速度とし、\( y \)を縦方向、上向きを正とした。

電極板の間に電子がいる時間\(t_1\)は

\begin{eqnarray} t_1 = \frac{L_1}{v_0} \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

であるので、電極板を抜ける時の\( y \)方向の速度は

\begin{eqnarray} v_y = a_y t_1 = - \frac{eE L_1}{m_e v_0}\ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

となり、電子が電極板の端を通る時の\( y \)方向の変位\( y_1 \)は

\begin{eqnarray} y_1 = \frac{1}{2} a_y t_1^2 = - \frac{1}{2} \frac{eE L_1^2}{m_e v_0^2}\ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

を得る。このようにして電極板の間での電子の運動の様子がわかった。次に電極板の端を抜けてからスクリーンまでの電子の運動を見ていく。電極板の端を抜けてからスクリーンまで到達する時間\(t_2 \)は

\begin{eqnarray} t_2 = \frac{L_2}{v_0}\ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}

であるので、電極板の端を抜けてからの\(y\)方向の変位\(y_2\)は

\begin{equation} y_2 = v_y t_2 = - \frac{eE L_1 L_2}{m_e v_0^2}\ \ \ \ \ \ \ \ \ \ \ \ (6) \end{equation}

である。観測されるのは水平位置からの変位である\( | y_1 + y_2| \)であるので、\( | y_1 + y_2 |\)の式にしてやることで、

\begin{eqnarray} | y_1 + y_2 | = \frac{eE L_1 L_2}{m_e v_0^2} + \frac{1}{2} \frac{eE L_1^2}{m_e v_0^2} = \frac{1}{2} \frac{eE L_1}{m_e v_0^2} (L_1 + 2L_2)\ \ \ \ \ \ \ \ (7) \end{eqnarray}

となる。これにより比電荷\( m / m_e \)は

\begin{eqnarray} \frac{e}{m_e} = \frac{2 v_0^2}{E L_1} \frac{| y_1 + y_2 |}{(L_1 + 2L_2)} \ \ \ \ \ \ \ \ (8) \end{eqnarray}

と表すことができるのである。

ここで、最後に未知数なのは電子の\(x\)方向の速度である\( v_0 \)だけとなった。これは図3のように横方向に磁場をかけてやることで求めることできる。

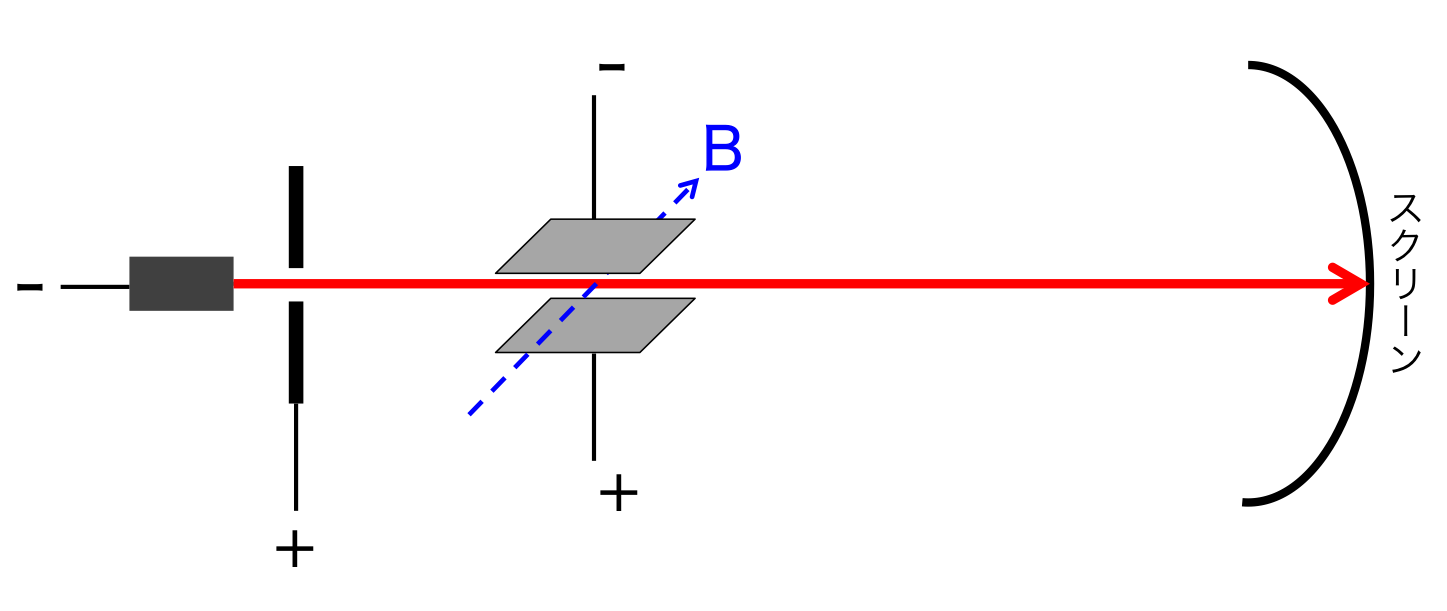
図3 電場による力と磁場によるロレンツ力を釣り合わせてまっすぐ電子を運動させた場合

電子が電極板で下向きに受ける力を相殺するように磁場によるローレンツ力をかけてやる。つまり、電子にかかる電場による力とロレンツ力を釣り合わせて、一切\( y \)方向に運動しないようにする。すると釣り合いの式から

\begin{eqnarray} eE = ev_0 B \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}

となり、

\begin{eqnarray} v_0 = \frac{E}{B} \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \end{eqnarray}

を導けるのである。この実験によってトムソンは比電荷を求めることに成功した。この後、ミリカンの実験により電気素量\( e \)が決定され、同時に電子の質量も明らかにされることになる。