クーロンポテンシャル(クーロンエネルギー)
カテゴリー:電磁気学
クーロンポテンシャルまたは、クーロンエネルギーとは、電気的な力によって生じる位置エネルギーのことである。
力学で位置エネルギーと言えば、重力\( mg \)に逆らって物体を持ち上げた高さ\( h \)を使って\( mg h\)と表される。
また、バネに付けられた質点を、バネによる力\( k \)に逆らって釣り合いの位置から移動させた距離\( x \)を使って\( kx \)と書ける。
どちらの場合も同じで、力が加えられている質点に対して、その力に逆らって(または従って)移動させた場合、位置エネルギーは大きくなるのである。
もしも、電荷が2つ以上存在した場合に、そこにはクーロンの法則によってクーロン力が生じる。
この場合も、重力やバネの場合と同様に、電荷には力が加えられているので、電荷は位置エネルギーを持つのである。
このクーロンの法則によって生じた力による位置エネルギーをクーロンポテンシャルと呼ぶ。
今、点Pから点Rまで電荷を移動させる場合を考える。
このときの位置エネルギー減少量は、点Pから点Rまでに行う仕事に等しいのである。これは、
\begin{eqnarray} W = - \int {\bf F} \cdot ds \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
であるためである。
つまり、点P, Rでの位置エネルギー(クーロンポテンシャル)を\( U_P \)、\( U_R \)とすると
\begin{eqnarray} U_P - U_R = W_{P\rightarrow R} = \int^R_P {\bf F} \cdot d{\bf s} = \int^{R}_{P} F_t ds \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
と表すことができる。 (式(2)は電場による力\( {\bf F} = q{\bf E} \)に沿って電荷を動かしていることに注意する。)
ここで、\( F_t \)は電荷の微小変化\( \Delta {\bf s} \)に沿った方向の力である。
つまり、\( F_t = F \cos \theta \)である。
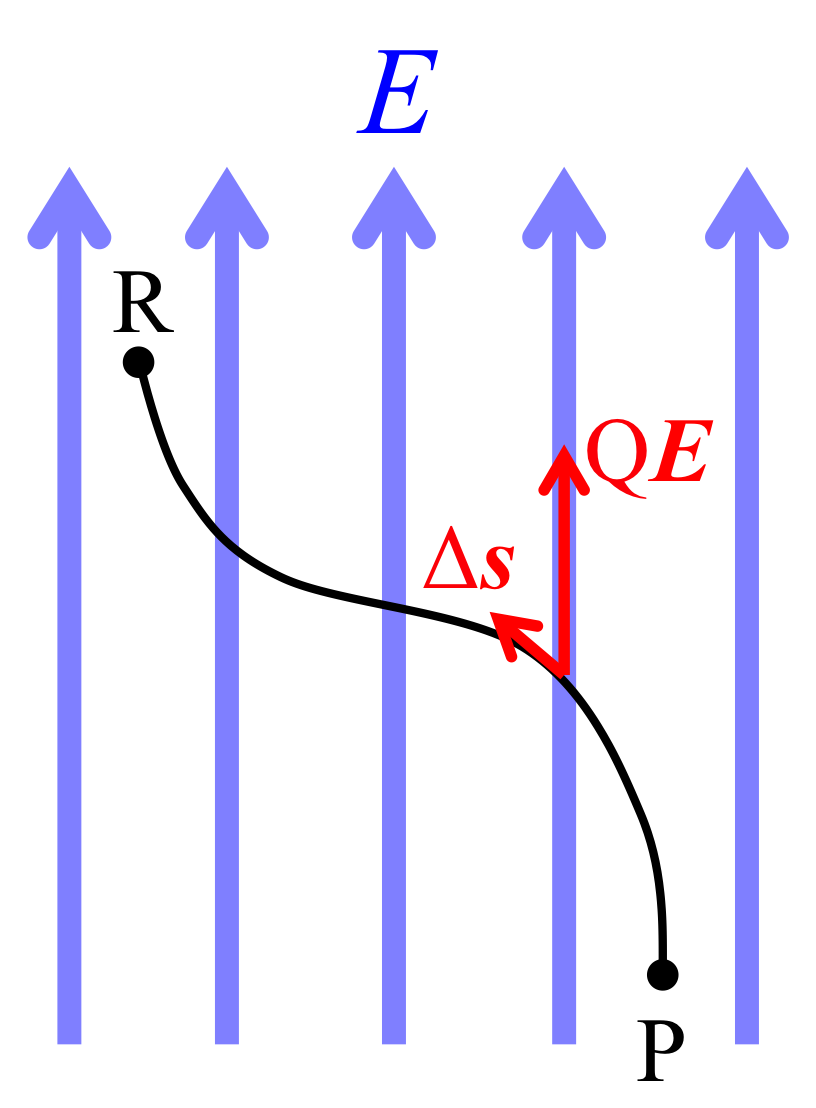
図1. 電場中を点Pから点Rへ移動する電荷の経路
図で示すと図1、2のようになる。
この時、点Pから点Rまで行く道筋はどのような経路を取っても仕事\( W_{P\rightarrow R} \)は変わらない。
もっというと、仕事\( W_{P\rightarrow R} \)は始点と終点の位置だけで決まるのである。
この性質が位置エネルギーを定義できる条件なのである。
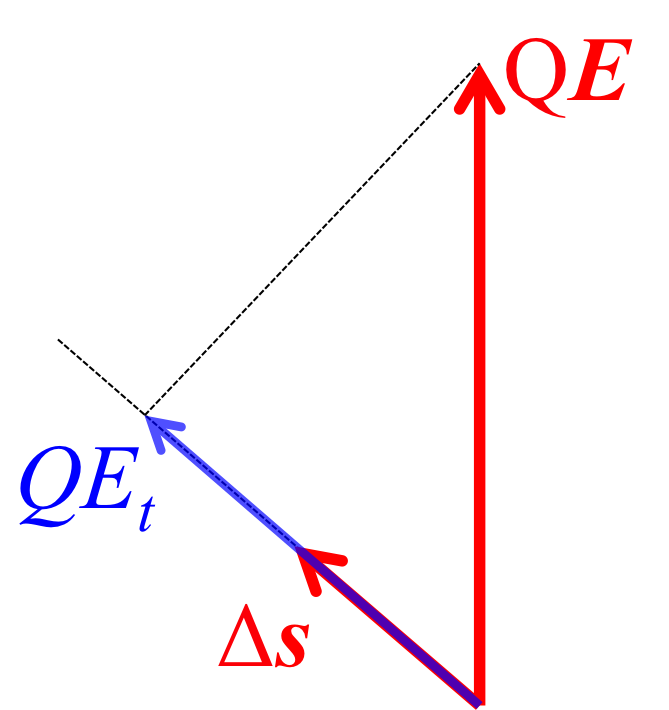
図2. 電荷にかかるベクトル
では実際にクーロンポテンシャルを求める。
2つの点電荷\( Q_1 \)と\( Q_2 \)がある場合を考える。 この時、互いの距離が\( r \)であった場合、力
\begin{eqnarray} F = \frac{Q_1 Q_2}{4 \pi \epsilon_0 r^2} \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
が働く。この力による位置エネルギー\( U(r)\)を求める。
式(3)を式(2)に代入する。
\begin{eqnarray} U(r_1) - U(r_2) = \int^{r_1}_{r_2} {\bf F} \cdot d{\bf s} = \frac{Q_1Q_2}{4 \pi \epsilon_0} \left( \frac{1}{r_1} - \frac{1}{r_2} \right) \ \ \ \ \ \ \ (4) \end{eqnarray}
となる。この時、\( r_1 = r\)、\( r_2 = \infty \)とすることで、クーロンポテンシャル
\begin{eqnarray} U(r) = \frac{Q_1Q_2}{4 \pi \epsilon_0 r} \end{eqnarray}
と求めることができる。
なぜ、\( r_2 \)を無限遠にとったかは疑問に残るかもしれない。
「位置エネルギー 無限遠」と検索するれば答えが載っているサイトはいっぱいあるので、ここでは簡単に述べるに留まる。
位置エネルギーはスカラー量で、変化があった場合、その差がわかればいい。 式(3)に示すように力は電荷同士の距離の2乗に反比例して小さくなる。
今、どれくらい位置エネルギーが増えたか知りたい場合、どの場所を基準とするのが良いのであろうか?
もし、電荷2が無限遠にあった場合はお互いに働く力は0となる。 この点を基準として考えようということで、\( r_2\)を無限遠にするのである。
つまりは、無限遠に離れていた電荷\( Q_1 \)と電荷\( Q_2 \)と\( r \)の距離まで近づけた時にする仕事という意味でクーロンポテンシャルを定義するのである。