無限に広がった平面に分布する電荷が作る電場
カテゴリー:電磁気学
無限に広がった平板に一様に分布する電荷が作る電場をガウスの法則を使って求める。 この時、平板の厚さは無視する。
まずはどの向きに電場が作られるのかを考える。 電荷は一様に分布しているので、平板に平行の電場成分は電荷分布の対称性から打ち消しあって消える。
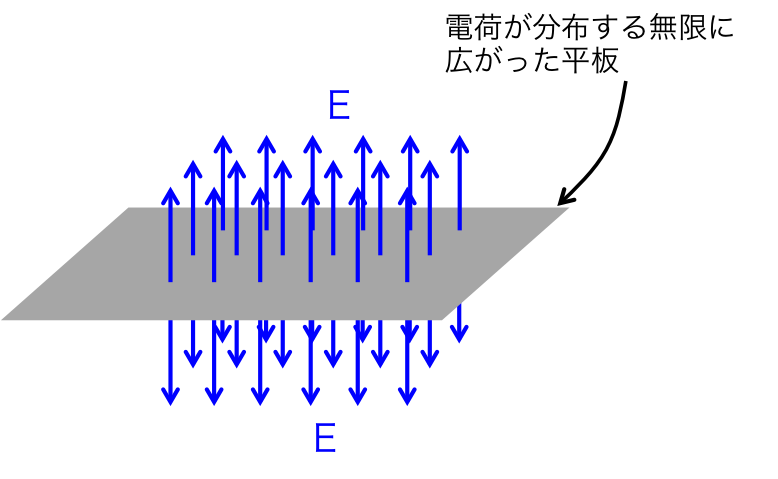
図1. 無限に広がった平板に一様に分布する電荷が作る電場
つまり、図1のように平板に垂直な電場のみができるのである。 図に示したのは正電荷の場合である。
また、図を見てわかるように電荷は平面の上下に作られる。 ガウスの法則を使って電場を求める際は電場に対して垂直な面と平行な面で構成される閉曲面を考えると便利である。
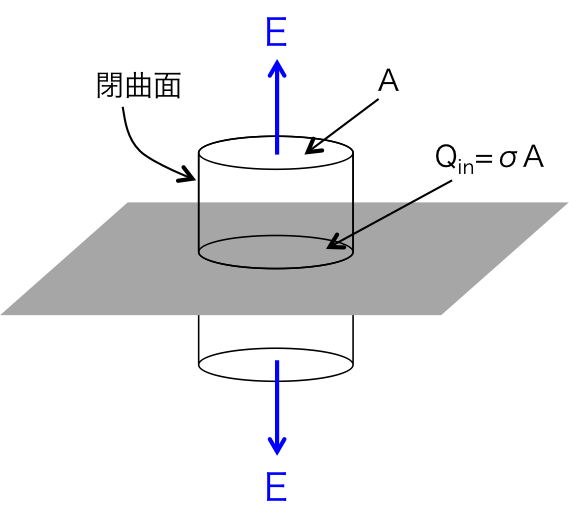
図2. ガウスの法則を求める際に設定する閉曲面
ここでは図2に示すような平面を貫く底面と下面の面積が\( A \)である円柱を考える。 では、実際にガウスの法則から電場を求める。
ガウスの法則は、
\begin{eqnarray} \iint_S {\bf E} \cdot d{\bf A} = \frac{Q_{in}}{\epsilon_0} \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
と表される。 式(1)の左辺は電場に垂直な面の面積と電場の掛け算で表される。
また、\( Q_{in} \)は閉曲面内部に含まれる電荷である。
まず、左辺では電場に垂直な面だけを考えればよくて、図2のとおり閉曲面の電場に垂直な面は上面と下面しかなく、その面積の合計は\( 2A \)である。
平板状に存在する電荷は、面密度を\( \sigma \)とすると、\( Q_{in} = \sigma A \)となるのである。 つまり、式(1)は、
\begin{eqnarray} 2A E = \frac{A\sigma}{\epsilon_0} \ \ \ \ \ \ \ \ (2) \end{eqnarray}
と解ける。以上のことから、無限に広がる平板に一様に分布する電荷が作る電場は、
\begin{eqnarray} E = \frac{\sigma}{2 \epsilon_0} \ \ \ \ \ \ \ \ (3) \end{eqnarray}
と求められる。
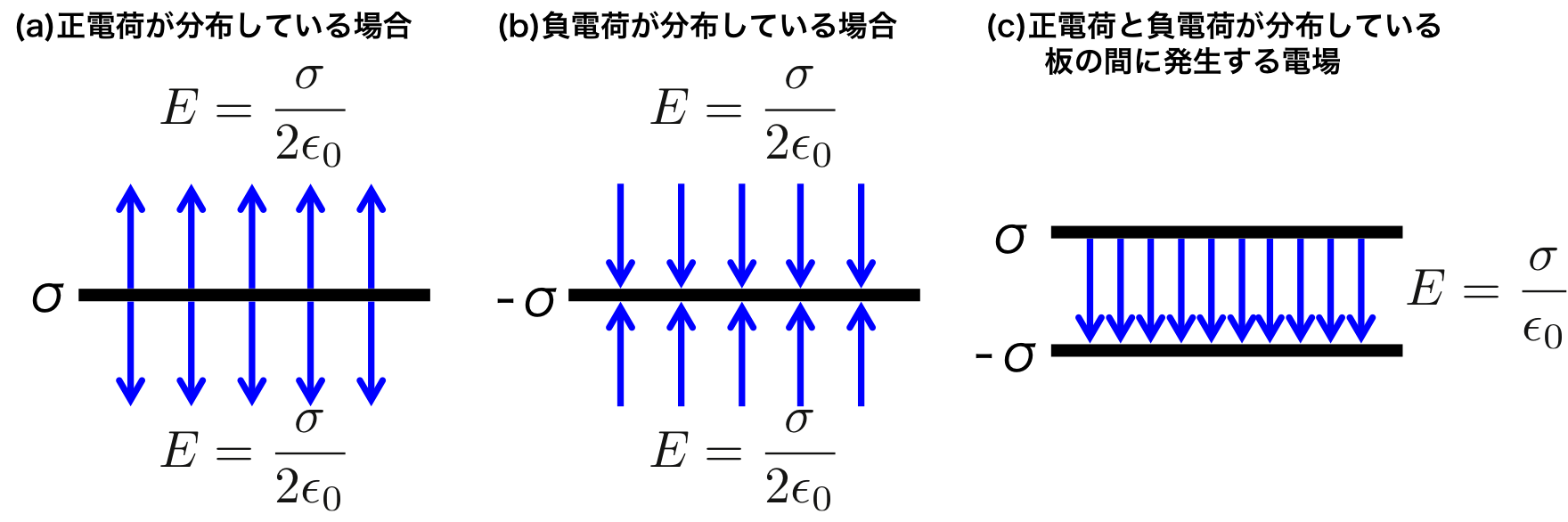
図3. (a)正電荷によって作られる電場、(b)負電荷によって作られる電場、(c)正電荷と負電荷が分布した平板の間に生じる電場
今は正電荷を想定して電場を求めた。 正電荷の場合は図1に示したように平板から出て行く方向に電場が作られる。
もし、負電荷が分布していた場合は電場の大きさは変わらないが電場は平板に突き刺さるように作られるのである。
また、正電荷が分布した平板と負電荷が分布した平板が互いに平行に向けられた場合、その間に発生する電場は式(3)を丁度2倍した電場が作られる。
これは図3を見てもらうと明らかだが、ガウスの法則を使って計算すると、平板の間に作られる電場は(a)と(b)の電場を足し合わせた形になるからである。