球対称に分布する電荷が作る電場

カテゴリー：電磁気学

よくあるガウスの法則を使って解く問題に、球対称に分布する電荷が作る電場を求める問題がある。

これは球の中に、電荷が、ある密度で満たされていて、その球の外では電荷が存在しない場合である。球内部の電荷の分布は対称（球対称）であるとする。

ガウスの法則を使って電場を求める。

まず、電荷が一様に分布する球の中心と同じ点を中心とする閉曲面を考える。閉曲面の半径を\( r \)とする。ガウスの法則は、

\begin{eqnarray} \iint_S {\bf E} \cdot d{\bf A} = \frac{Q_{in}}{\epsilon_0} \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

と表される。この時、左辺は閉曲面に垂直な電場成分と閉曲面の面積の掛け算となる。

右辺の\( Q_{in} \)は閉曲面内部に存在する電荷の総量である。

つまり、

\begin{eqnarray} E 4\pi r^2 = \frac{Q_{in}}{\epsilon_0} \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

を得る。この式を解くことで、

\begin{eqnarray} E = \frac{Q_{in}}{4\pi \epsilon_0 r^2} \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

を得る。ここで、電荷の存在は球対称であるので、閉曲面に垂直な電場以外の電場の成分は存在しない。

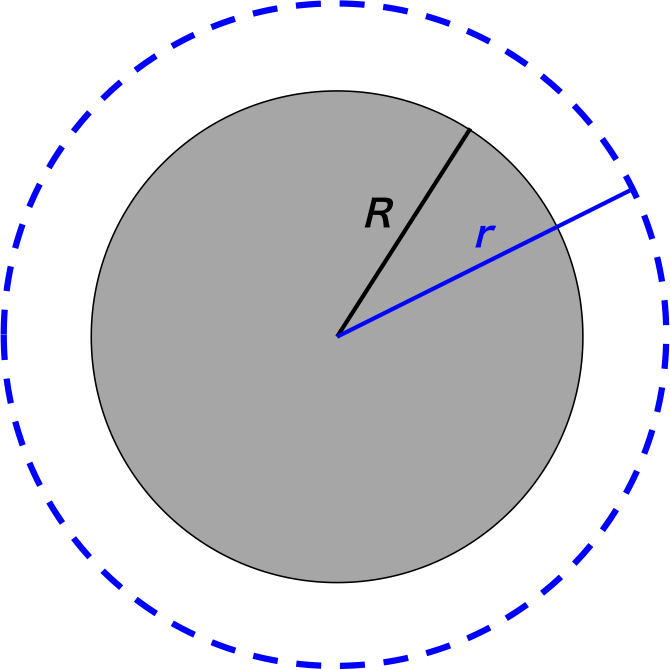
図1.　一様に分布した電荷と電荷が存在する球外部の閉曲面の断面

もし、閉曲面を電荷が分布している球の外側に取った場合を考える。図1にその断面を示している。

この場合、閉曲面内の電荷\( Q_{in} \)は、

\begin{eqnarray} Q_{in} = \frac{4}{3} \pi R^3 \rho \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

と表される。ここで、\( R \)は電荷が分布している球の半径である。

これを式(3)に代入することで、電場を

\begin{eqnarray} E = \frac{R^3 \rho}{3 \epsilon_0 r^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}

と求めることができる。

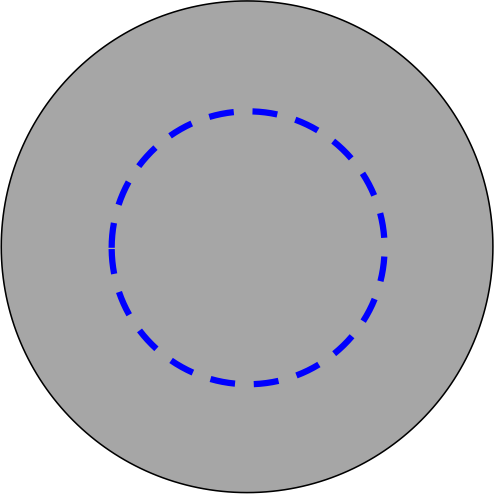
図2.　一様に分布した電荷と電荷が存在する球内部の閉曲面の断面

次に、閉曲面が図2のように電荷が存在する球の内部に取る場合を考える。この時、閉曲面内部の電荷\( Q_{in} \)は、

\begin{eqnarray} Q_{in} = \frac{4}{3} \pi r^3 \rho \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
である。これを式(3)に代入することで、

\begin{eqnarray} E = \frac{r \rho}{3 \epsilon_0}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}

と求めることができる。上記のように球内部に一様に存在する電荷が作る電場は、球内部と外部で異なるのである。

以上のことをまとめると、

\begin{eqnarray} E =\left\{ \begin{array}{ll} \frac{R^3 \rho}{3 \epsilon_0 r^2} & (r>R) \\ \frac{r \rho}{3 \epsilon_0} & (r \le R) \end{array} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}

となるのである。この場合は球対称で取り扱いやすい場合を扱ったが、ガウスの法則を用いることで電荷分布からそこに現れる電場の大きさを求めることができるのである。