静電場の渦なしの法則

カテゴリー：電磁気学

ガウスの法則の微分系は、電場の発散で表されることを学んだ。

電場の回転（\( \mathrm{rot} \)）も電磁気では重要な意味を持つ。

先に答えから言うと、電場の回転は0になる。つまり、

\begin{eqnarray} \nabla \times {\bf E} = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

ということである。

これは、電場は正電荷から湧き出て負電荷に入っていくか、無限遠まで伸びていくと言うことを意味するのである。

この電場の回転が0になるという法則を渦なしの法則と呼ぶ。

ちなみに、渦なしの法則が成り立つのは、静電場の場合においてだけである。

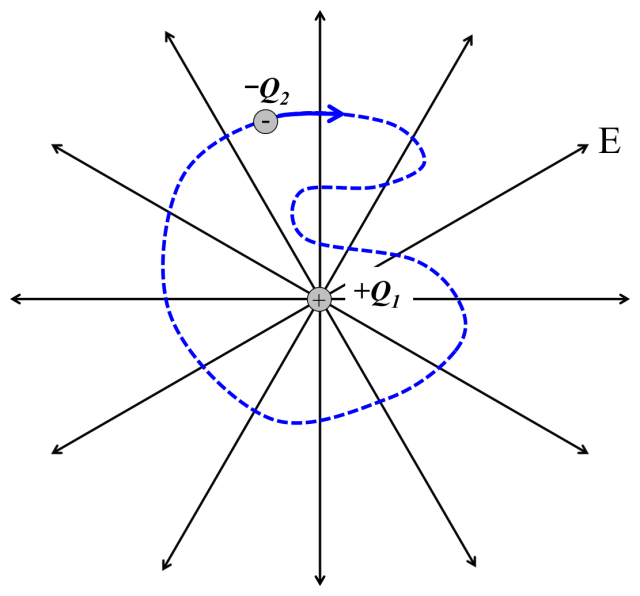
図1.　正電荷\(Q_1\)から出る電気力線と、そこに置かれた負電荷\(Q_2\)。

では、静電場の渦なしの法則を求めていこうと思う。

まずは、図1のように正電荷\( Q_1\)が作る電場中に負電荷\( Q_2 \)を置いた場合を考える。

この時、それぞれの電荷の正負はどちらでも結果は一緒になる。

また、負電荷\( Q_2 \)が作る電場は話を簡単にするために今は描かれていない。

この負電荷\( Q_2 \)を青の点線のように途中で途切れることのない閉じた経路に沿って移動させる。

すると、ちょうど１周にかかる仕事の量は必ず0になる。つまり、

\begin{eqnarray} \oint_C {\bf F} \ dl = 0 \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

ということなのである。（ちなみにこの積分は円積分と呼び、閉じた経路を1周分積分すると言うことである。）

これは当たり前のことで、経路に沿って仕事が正になった場合は、その経路に沿って無限に加速してしまい、エネルギーの保存則が成り立たない。

もっと言うと、もし負電荷が経路1周の間に加速されていたとすると、同じ場所に戻ってきていて位置エネルギーは変化していないのに、運動エネルギーは増加してしまっていることになるのである。

よって、電荷を静電場中の閉じた経路を移動させた場合その仕事は0になるのである。

式(2)の\( {\bf F} \)は電場中の電荷に加わる力であるので、\( {\bf F} = -Q_2 {\bf E} \)となるのである。つまり、

\begin{eqnarray} \oint_C {\bf E} \ dl = 0 \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

と変化できる。式(3)は、線積分であるので、ストークスの定理を使って面積分に変化させる。すると、

\begin{eqnarray} \oint_C {\bf E}\ dl = \iint_S \nabla \times {\bf E}\ dA = 0 \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

となる。ここで、Sは閉曲面で\(dA\)は閉曲面S上の微小平面である。

この式(3)がどの閉曲面を選んでも成り立つためには、

\begin{eqnarray} \nabla \times {\bf E} = 0 \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}

でなければならない。このようにして、を得ることができるのである。

また、式(4)を渦なしの法則の積分系、式(5)を渦なしの法則の微分系と呼ぶこともある。