一様な電場の電気力線束
カテゴリー:電磁気学
電気力線は通常、その密度が電場の強度に比例するように描かれる。 電場の強度に対する電気力線の密度に厳密な決まりがあるわけではないが、このページではわかりやすいように、 1 N/Cの電場では、電場の向きに垂直な面積 1 m\(^{2}\)の平面を電気力線が1本貫くものとする。 (これはこのページの説明を楽にするための仮定であり、物理的な厳密な決まりはない。) この時、図1のように電場に対して垂直に立てた平板Sを考える。
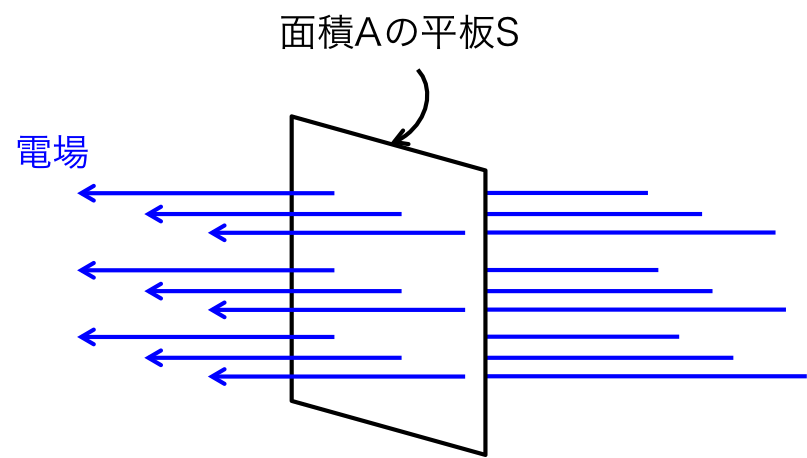
図1.電場に垂直に立てられた面積Aの平板S
平板Sは面積Aとする。この時、電場は渦を巻かないとする。 つまり、図1で青線で示した電気力線は曲がらず直線で表される。 もし、上で定義したように1 N/Cの電場では電場の向きに垂直な面積 1 m\(^{2}\)の平面を電気力線が1本貫くとすると、面積Aの平板Sを貫く電気力線の数\( \Phi_E \)は \begin{eqnarray} \Phi_E = EA \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} と表される。
もし、平板Sが電場に対して傾いていた場合はどうなるだろうか?
想像すれば簡単にわかるが、電場に対して垂直に平板Sを立てた場合より、平板Sを貫く電気力線は必ず減ることになる。

図2.電場に対して\( \theta \)で立てられた面積Aの平板S
図2のように電場に対する傾き\( \theta \)を取ると、平板Sを貫く電気力線の数\( \Phi_E\)は
\begin{eqnarray} \Phi_E = EA \cos \theta \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}となるのである。
ここで法線ベクトルというものを導入する。 法線ベクトルとは通常\( {\bf n} \)で表され、今考えられている面に対して垂直で大きさが1のベクトルのことである。 図で表すと図3のようになる。

図3. 法線ベクトル\( {\bf n} \)
この法線ベクトルは平板Sに対して垂直であるので、もし電場ベクトルとの内積をとった場合
\begin{eqnarray} {\bf E} \cdot {\bf n} = En\cos \theta = E \cos \theta \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}となるのである。つまり、式(2)は
\begin{eqnarray} \Phi_E = {\bf E} \cdot {\bf n} A \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}とスマートな形に書き換えることができる。 または、\( {\bf A} = A {\bf n} \)とすることで
\begin{eqnarray} \Phi_E = {\bf E} \cdot {\bf A} \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}とより一層スマートな表現方法になるのである。 式(4)と(5)のように表現すると、電気力線の本数\( \Phi_E \)がマイナスになることがある。 これは、電場と法線ベクトルの成す角度が90度以上になった場合である。 これは図3で示した法線ベクトルがある面を表面とすると、\( \Phi_E \)がマイナスになったということは、表から裏に電気力線が貫いていることを意味するのである。 式(3)のようにスカラーで記述するよりも、ベクトルで記述した方がこのように面に対してどの向きに電気力線が貫いているのかも知ることができるのである。