ミリカンの実験
カテゴリー:電磁気学
すべての電荷は電気素量の整数倍となる。これは物理現象の中でも特に不思議な特性の一つであるが、いったい誰が気づいたのであろうか?
1909年、ロバート・ミリカンは後にミリカンの実験として有名になる電子の電荷を測定する実験で、電荷が常にある特定値の整数倍になること、その特定値である電気素量を明らかにした。
ミリカンは、この功績により1924年にノーベル物理学賞を受賞している。
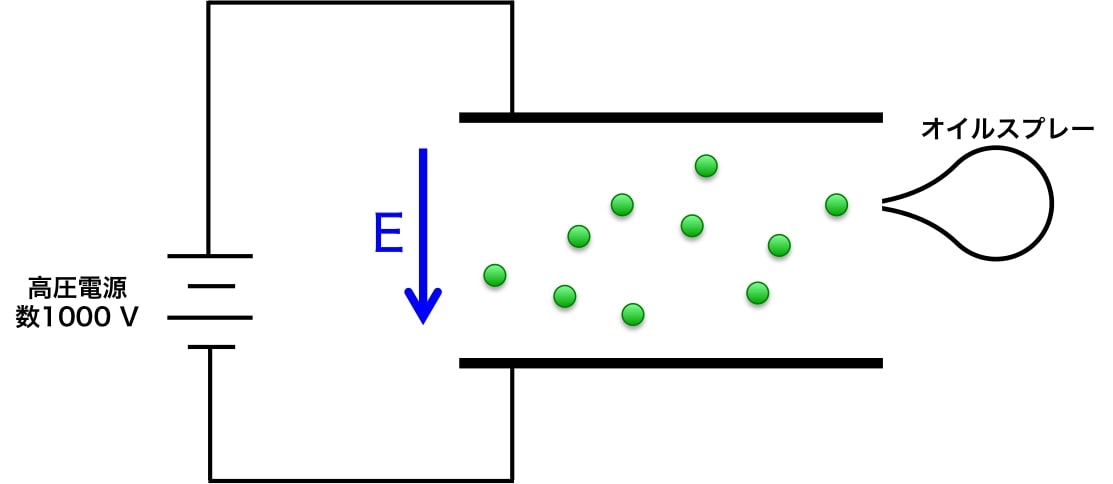
図1 ミリカンの実験装置
図1に示した物がミリカンの実験の器具である。
ミリカンは電極間に高電圧を掛け、電場を作り、そこに帯電させた油滴を噴霧させた。 (油を油滴にする際に摩擦を使って帯電させる。)
帯電させられた油滴には、電子が何個かくっついている。
電極間に投入された油滴は、ゆっくり降下していく。
その時、空気抵抗と重力が釣り合い、すぐに終端速度に達して等速度で降下する。 (終端速度に達する時間は1秒より極めて短い。)
次に電場をかけると、電子がくっついて負に帯電している油滴は\( qE \)の力によって、上向きの力を受ける。
この上向きの力を重力を超えるほどかけることで、油滴は上昇を始めるのである。
この上昇速度は、油滴の電荷に比例するので、上昇速度を何回も測定することで、電気素量を求めることができる。
ミリカンの実験では、油滴を丁度静止させる電場を印加したが、丁度の電場をかけるのは非常に難しいので、ここではミリカンの実験に非常に近い形で、簡単に素電荷を求める方法を紹介する。
現在の大学の授業で行われているミリカンの実験は、ほとんどがこの方法である。
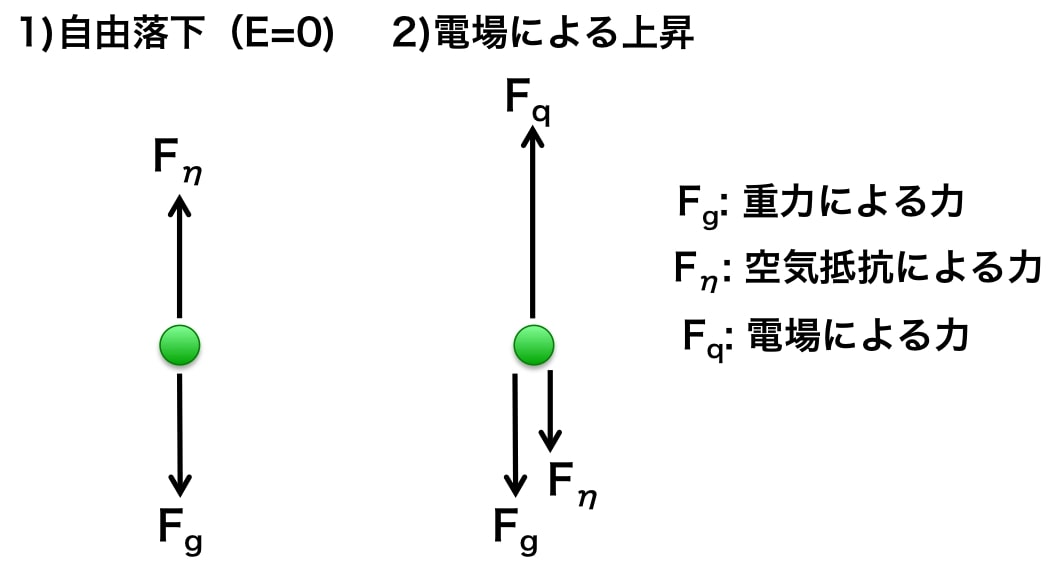
図2 電極内の油滴にかかる力
図2では、電極に噴射された油滴を表し、電場がかけられた場合と電場がかけられていない場合を示す。
この油滴にかかる力は、重力による力\( F_{g}\)、空気抵抗力\( F_{\eta} \)、電場による力\( F_{q} \)である。
それぞれの式を記述すると、
となる。
ここで、\( \rho \)は油の密度、\( \eta \)は空気の粘性係数、\( v \)は油滴の速度、\( E \)は電場を表す。
電場がかかっていない(1)の場合と電場がかけられた(2)の場合の力の釣り合いの式を導出する。
油滴は終端速度に達しており、等速運動をしているので、図2のように力は釣り合った状態になっている。
下降する速度を\( v_0 \)、上昇する速度を\( v_u \)とすると、
を導くことができる。
この2式で未知数は\( q \)と\( r \)だけである。 \( q \)について解くことで、素電荷を求めることができる。
まず、式(4)から油滴の半径は
を得る。
これを、式(5)に代入することで、
を導くことができる。
ミリカンの実験によって、上昇速度\( v_u \)と下降速度\( v_0 \)を測定することで素電荷を求めることができるのである。
ミリカンの実験で最も工夫したと考えられる点は、油滴を空気中に放出したことではないだろうか?
物理実験は、空気の抵抗を無視するために真空中で行うことが多いが、ミリカンの実験はあえて空気中で行うことで、終端速度から等速運動を作り出し、 運動方程式を簡単にしているのである。
スポンサーリンク