円盤上に分布する電荷が作る電場
カテゴリー:電磁気学
円盤に電荷が密度\( \rho \)で一様に分布している。 この電荷が\(z\)軸に作られる電場を求める(図1)。
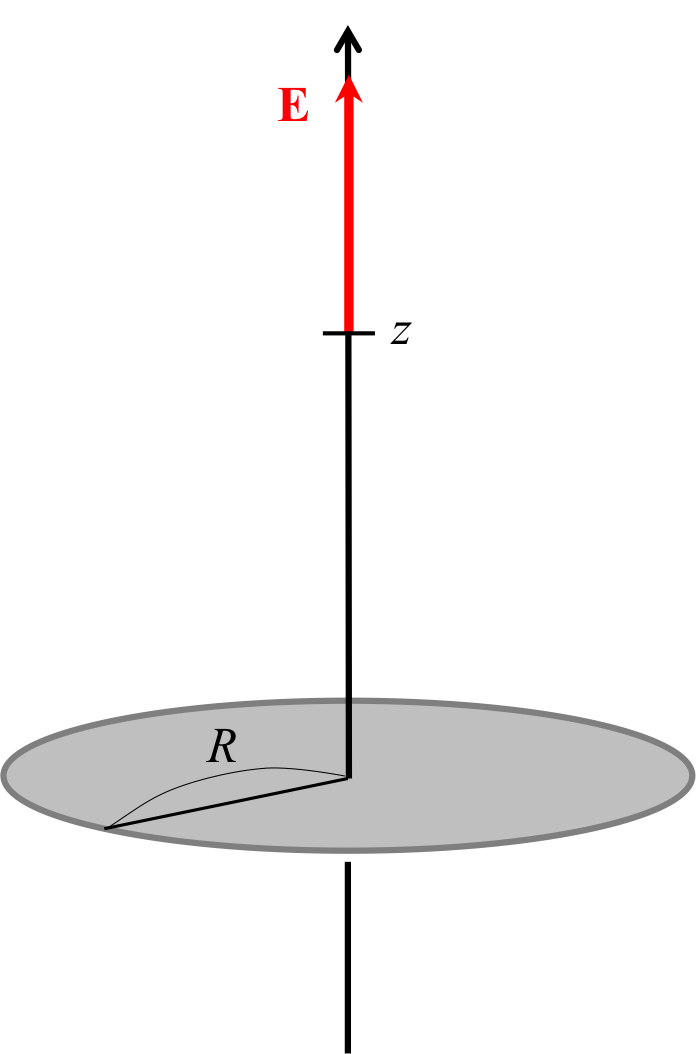
図1. 円盤上に分布する電荷が\( z \)の位置に作る電場
半径\( r \)の円周上に一様に分布した電荷が\( z \)軸上に作る電場\( dE \)は、 \begin{eqnarray} dE = \frac{2\pi r \rho z dr}{4 \pi \epsilon_0 (r^2 + z^2)^{3/2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} で表される。この時、幅\( dr \)、半径\( r \)の円環に含まれる電荷の総量は\( 2\pi r \rho dr \)である。
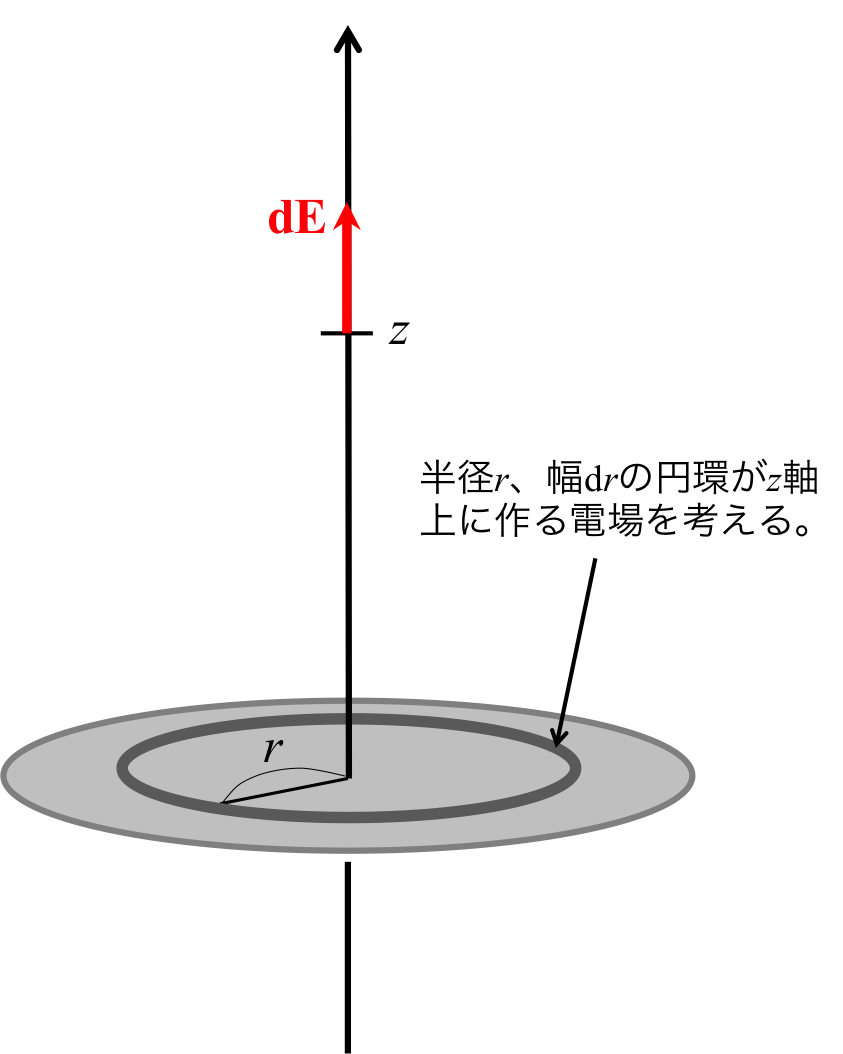
図2. 幅\( dr \)の円環が\( z \)の位置に作る電場
式(1)を整理すると、 \begin{eqnarray} dE = \frac{ \rho z}{2 \epsilon_0} \frac{r}{(r^2 + z^2)^{3/2}}\ dr \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} となるのである。この\( dE \)を0から\(R\)まで積分することで、円盤上に密度\( \rho \)で一様に分布している電荷が\( z \)軸上につくる電場を求めることができる。 \begin{eqnarray} E &=& \int^{R}_0 \frac{ \rho z}{2 \epsilon_0} \frac{r}{(r^2 + z^2)^{3/2}}\ dr \\ &=& - \frac{ \rho z}{2 \epsilon_0} \left[ \frac{1}{(r^2 + z^2)^{1/2}} \right]^{R}_0 \\ &=& - \frac{ \rho z}{2 \epsilon_0} \left\{ \frac{1}{(R^2 + z^2)^{1/2}} - \frac{1}{ z } \right\} \\ &=& \frac{ \rho }{2 \epsilon_0} \left\{ 1 - \frac{z}{(R^2 + z^2)^{1/2}}\right\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} もし円盤の半径\( R \)が\( z \)に対して十分に大きい時、式(3)の括弧内の第二項は0に収束する。 すると、\( R >> z \)の時\( z \)軸上の電場は、 \begin{eqnarray} E = \frac{ \rho }{2 \epsilon_0} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} と近似できるのである。