円周上に分布する電荷が作る電場

カテゴリー：電磁気学

円周上に電荷が一様に分布しており、その全量が\( Q \)の場合を考える。 また、円の幅は無視することとする。 図1のように円周上の微小区間\( ds \)が\( z \)軸上の点に作る電場は、 \begin{eqnarray} dE = \frac{dQ}{4 \epsilon_0 \pi r^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} と書くことができる。 水平方向の電場は、円周の180度反対の電荷が作る電場と打ち消しあうため、円周上全ての電荷が作る電場を計算する際に消える。 つまり、円周上の電荷が作る電場の計算は、\( z\)軸上に作られる電場を計算するのみで良い。 \(z\)軸上の電場は \begin{eqnarray} dE \cos \theta = \frac{\cos \theta dQ}{4 \epsilon_0 \pi r^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} となる。

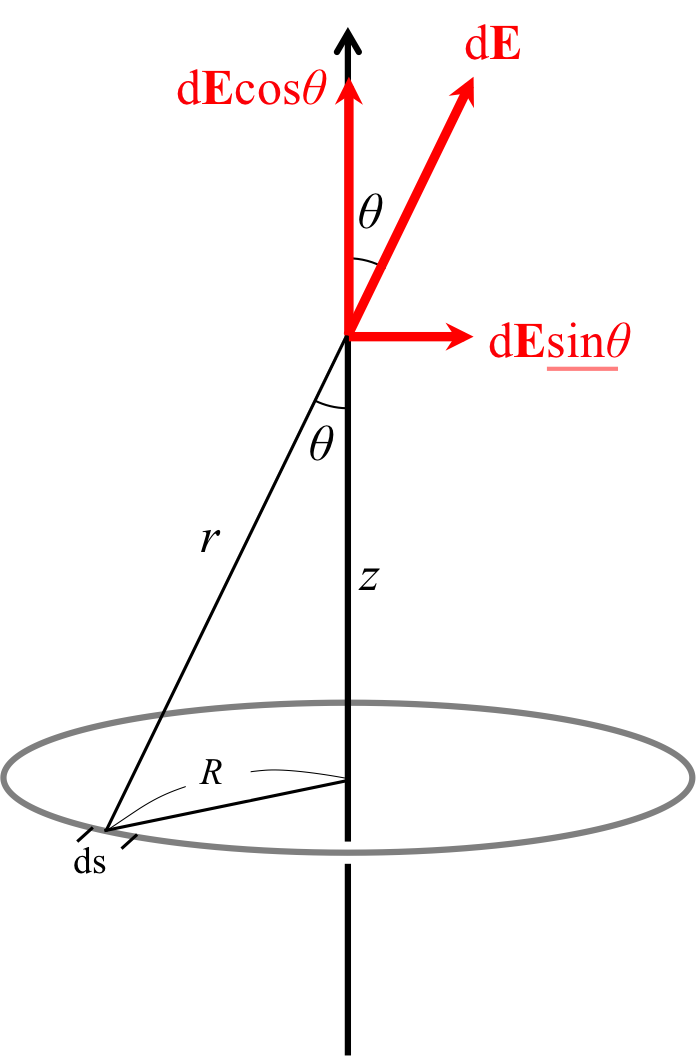
図1.　円周上に分布する電荷が\( z \)の位置に作る電場

この電場（\( dE\cos \theta \)）を円周分足し合わせてやることで、\( E \cos \theta = \cos \theta \Sigma\ dE \)で表される。 つまり、 \begin{eqnarray} E \cos \theta &=& \cos \theta\ \Sigma dE \\ &=& \frac{\cos \theta\ \Sigma dQ}{4 \pi \epsilon_0 r^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} となる。ここで、 \begin{eqnarray} \cos \theta = \frac{z}{r} = \frac{z}{(R^2 + z^2)^{1/2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} であることと、\( \Sigma dQ \)は円周上の全ての電荷の足し合わせであり、\( Q \)と表されることを用いて、円周上に一様に分布する電荷が\( z\)軸上に作る電場は、 \begin{eqnarray} \frac{Qz}{4 \pi \epsilon_0 (R^2 + z^2)^{3/2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} と表される。