電気双極子

カテゴリー：電磁気学

近接した正負の電荷のペアのことを電気双極子と呼ぶ。 この電荷のペアは周りに電場を作るのである。どのような電場を作るのか見ていこうと思う。

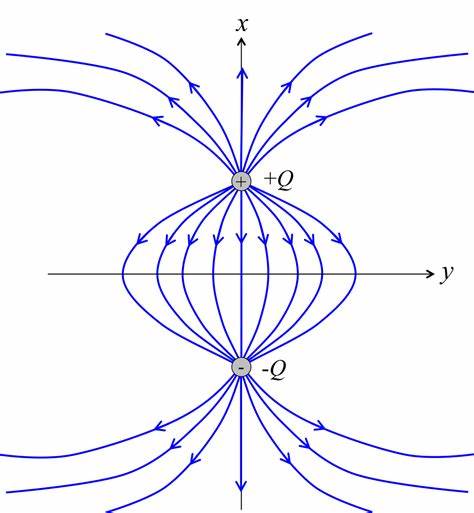
図1.　2つの近接した電荷（電気双極子）が作る電場

図1のように、\(x-y\)平面に電荷が置かれているとする。 ここで、縦軸を\( x \)軸としていることに注意する。 電荷の座標は正電荷\( Q \)が\( (a,\ 0,\ 0) \)、負電荷\( - Q \)が\( (-a,\ 0,\ 0) \)に置かれている。 座標\( (x_1,\ y_1,\ z_1) \)に置かれた電荷\(Q\)が\( (x,\ y,\ z) \)に作る電場の\(x\)成分、\(y\)成分、\(z\)成分、\(E_x\)、\(E_y\)、\(E_z\)は、 \begin{eqnarray} E_x &=& \frac{Q}{4 \pi \epsilon_0} \frac{x - x_1}{\left\{ (x-x_1)^2 + (y-y_1)^2 + (z-z_1)^2 \right\}^{3/2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \\ E_y &=& \frac{Q}{4 \pi \epsilon_0} \frac{y - y_1}{\left\{ (x-x_1)^2 + (y-y_1)^2 + (z-z_1)^2 \right\}^{3/2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \\ E_z &=& \frac{Q}{4 \pi \epsilon_0} \frac{z - z_1}{\left\{ (x-x_1)^2 + (y-y_1)^2 + (z-z_1)^2 \right\}^{3/2}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} と表される。 この方程式に図1に示した電荷の座標を代入することで、電場の大きさの\( x,\ y, z\)成分を得る。 \begin{eqnarray} E_x (x,\ y,\ 0) &=& \frac{Q}{4 \pi \epsilon_0} \left[ \frac{ x-a }{ \left\{ (x-a)^2 + y^2 \right\}^{3/2} } - \frac{ x+a }{ \left\{ (x+a)^2 + y^2 \right\}^{3/2} } \right]\ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \\ E_y (x,\ y,\ 0) &=& \frac{Q}{4 \pi \epsilon_0} \left[ \frac{ y }{ \left\{ (x-a)^2 + y^2 \right\}^{3/2} } - \frac{ y }{ \left\{ (x+a)^2 + y^2 \right\}^{3/2} } \right] \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \\ E_z (x,\ y,\ 0) &=& 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} ここで、\( r^2 = x^2 + y^2 \)、\( x = r \cos \theta \)、\( y = r \sin \theta \)とおく。 すると以下の関係を導ける。

ここで、\( r >> a \)とすることで、\( a^2/r^2 \approx 0\)とできる。 また、\( |x|<<1 \)の時、テイラー展開を用いることで、\( (1+x)^n \approx 1 + nx \)と近似することができる。 この関係を使うことで、式(7)は \begin{eqnarray} \frac{ 1 }{ \left\{ (x-a)^2 + y^2 \right\}^{3/2} } &=& \frac{1}{r^3 \left( 1 - 2 \frac{a}{r}\cos \theta + \frac{a^2}{r^2}\right)^{3/2}} \\ &\approx & r^{-3} \left( 1 + 3\frac{a}{r}\cos \theta \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray} と書き換えることができる。また、同様にして、 \begin{eqnarray} \frac{ 1 }{ \left\{ (x+a)^2 + y^2 \right\}^{3/2} } &\approx& r^{-3} \left( 1 - 3\frac{a}{r}\cos \theta \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray} の関係式を得ることができる。 この関係式(8), (9)を式(4), (5)に代入することで、 \begin{eqnarray} E_x &\approx& \frac{p}{4 \pi \epsilon_0 r^3} \left( 3 \cos^2 \theta - 1 \right)\ \ \ \ \ \ \ \ \ \ \ \ (10) \\ E_y &\approx& \frac{3p}{4 \pi \epsilon_0 r^3} \sin \theta \cos \theta\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) \end{eqnarray} を得るのである。

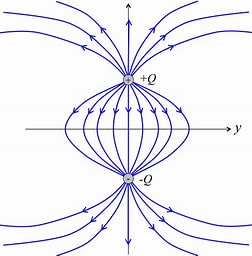
図2.　電気双極子が巨視的に作る電場

これは、\( p = 2Qa \)であり、電気双極子モーメントと呼ばれる。これは別のページで説明する。

式(10), (11)はどのような電場を示すのか考えようと思う。 式(10), (11)を導出する際に、\( r >> a \)とおいた。 これは電荷同士の距離\( 2 a \)より十分大きい距離\( r \)での電場のことを意味する。 こういった場合は「巨視的」と呼ぶ。 巨視的に見た場合の電気双極子の電気力線を図2に示す。 巨視的に見た場合、正負の電荷はほぼ原点に存在できると近似できるのである。 式(10), (11)で示される電場は電気力線の接線成分となるのである。

尚、式(10), (11)を極座標表示すると、 \begin{eqnarray} E_r &=& \frac{2p \cos \theta}{4 \pi \epsilon_0 r^3} \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \\ E_{\theta} &=& \frac{p \sin \theta}{4 \pi \epsilon_0 r^3} \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13) \end{eqnarray} となり直感的にわかりやすい形になる。