電場の重ね合わせ

カテゴリー：電磁気学

電荷が置かれるとその周りには必ず電場ができる。 1つの電荷だけの場合は、その電荷がつくる電場のみを考えればよかったが、もし電荷が2つ以上あった場合は、それぞれの電荷がそれぞれの電場を作るのである。

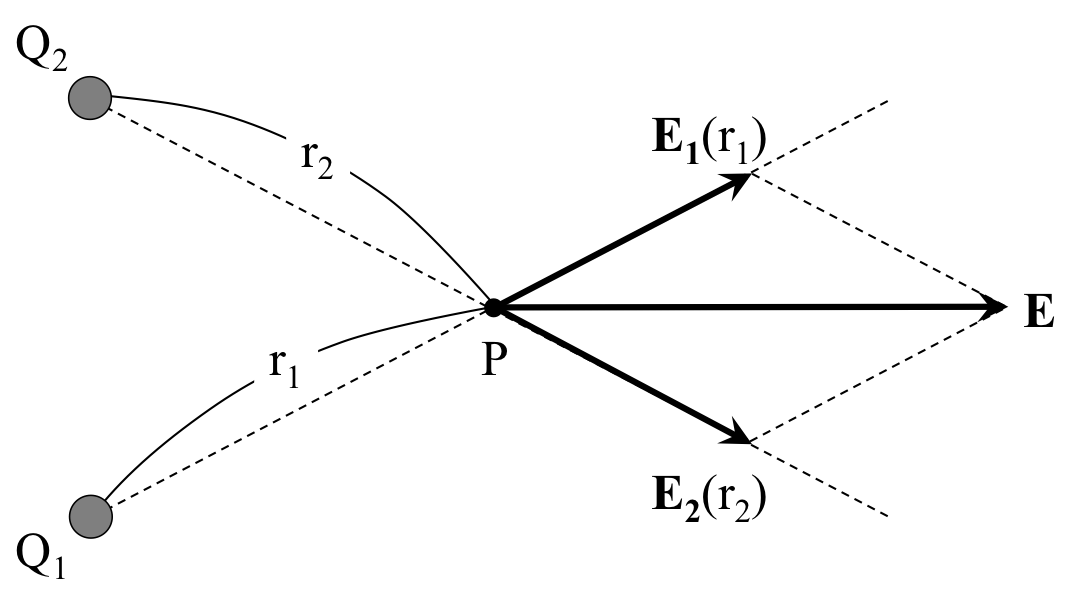
図1.　電荷\(Q_1\)と電荷\( Q_2 \)が点Pに作る電場

図1のように2つの電荷が置かれていた場合、点Pに作る電場は、 \begin{eqnarray} {\bf E} = {\bf E}_1(r_1) + {\bf E}_2(r_2)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} となるのである。式(1)の第1項は電荷\( Q_1 \)が作る電場で、第2項は電荷\( Q_2 \)が作る電場である。 このように各電荷が作る電場のベクトルを足し合わせたものがその点での電場となる。

もし、\( N \)個の電荷があった場合は、 \begin{eqnarray} {\bf E} = {\bf E}_1(r_1) + {\bf E}_2(r_2) + {\bf E}_3(r_3) + \cdots + {\bf E}_N(r_N)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} となる。このように個々の点電荷がある時に作られる電場は個々の点電荷の作る電場ベクトルの和で表される。 これを、電場の重ね合わせと言う。