電荷が作る電場
カテゴリー:電磁気学
電荷を空間上に置くと、そこには電場が生成される。 電場が光の速度で空間を伝搬していき、やがて無限遠まで広がっていく。 ここでは、電荷\( Q_1 \)が空間に置かれた時、どのくらいの大きさの電場が作られるのかを説明していく。
図1のように同じ符号の電荷\( Q_1 \)と電荷\( Q_2 \)が置かれている場合を考える。 この場合、それぞれの電荷が電場を生成し、相手の電荷に対して力を及ぼすが、この場合では電荷\( Q_1 \)が電荷\( Q_2\)の位置に作る電場を考えていく。 電荷\( Q_2 \)は電荷\( Q_1 \)からクーロン力\( {\bf F} \)は、 \begin{eqnarray} {\bf F} = \frac{1}{4\pi \epsilon_0} \frac{Q_1Q_2}{r^2} {\bf \hat{r}}\ \ \ \ \ \ \ \ \ (1) \end{eqnarray} である。ここで、\( Q_1 \)と\( Q_2 \)の距離を\( r \)として、クーロン力の方向の単位ベクトルを\( {\bf \hat{r}} \)とした。
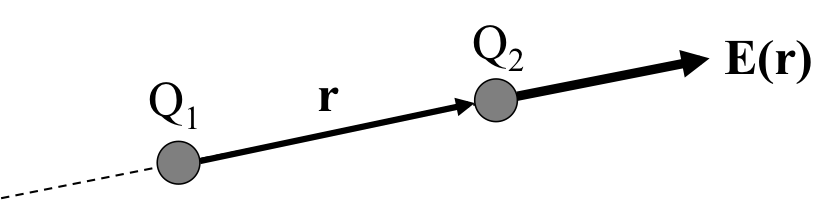
図1. 電荷\(Q_1\)が電荷\( Q_2 \)の位置に作る電場
この時、電荷\( Q_2 \)が電場から受ける力は、 \begin{eqnarray} {\bf F} = Q_2 {\bf E}({\bf r})\ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} と表される。この\( {\bf F} \)は、まさにクーロン力のことである。 式(1)と式(2)から、電荷\( Q_1 \)が電荷\( Q_2 \)の位置に作る電場は \begin{eqnarray} {\bf E}({\bf r}) = \frac{1}{4\pi \epsilon_0} \frac{Q_1}{r^2} {\bf \hat{r}}\ \ \ \ \ \ \ \ \ (3) \end{eqnarray} と表される。このとき、電場の大きさ\( E(r) \)は、 \begin{eqnarray} E(r) = \frac{1}{4\pi \epsilon_0} \frac{Q_1}{r^2} \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} である。(大きさだけを表せば良いので、式(3)から単位ベクトルを取っただけである。)
電場のベクトル表記
電荷が作る電場のベクトル表記を考えてみる。図1を状況から座標系で示してみる。 図2のように、電荷\( Q_1 \)と電荷\( Q_2 \)の位置ベクトルを、\( {\bf r}_1 \)、\( {\bf r}_2 \)とする。 ここで、\( O \)は原点である。
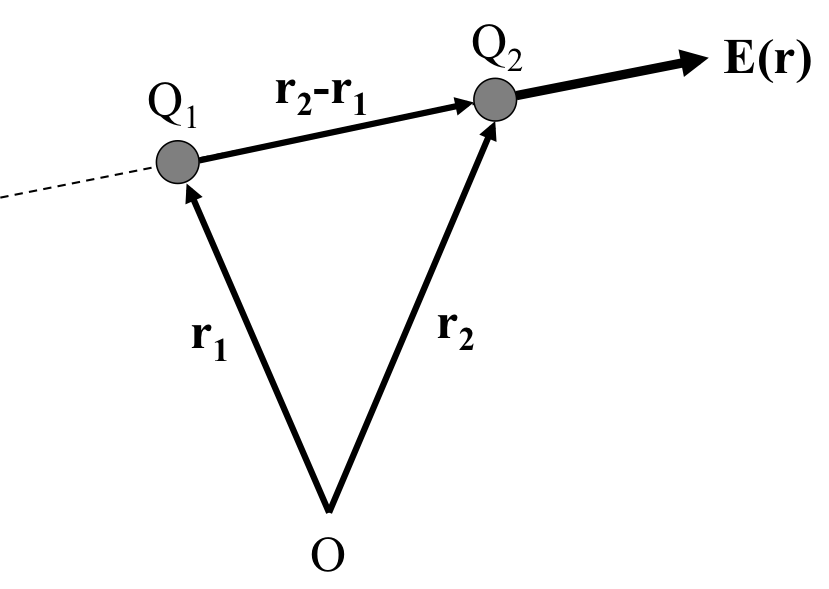
図2. 電荷\(Q_1\)が電荷\( Q_2 \)の位置に作る電場
\( Q_1 \)から\( Q_2 \)に向かうベクトルは、\( {\bf r}_2 - {\bf r}_1 \)と表される。 式(3)の\( Q_1 \)と\( Q_2 \)の距離\( r \)は、\( \left| {\bf r}_2 - {\bf r}_1 \right| \)と表され、距離ベクトルの単位ベクトルは、 \begin{eqnarray} {\bf \hat{r}} = \frac{ {\bf r}_2 - {\bf r}_1 }{\left| {\bf r}_2 - {\bf r}_1 \right|}\ \ \ \ \ \ \ \ (5) \end{eqnarray} と表すことができる。これらの関係式から、電荷\( Q_1 \)が電荷\( Q_2 \)に作る電場のベクトルは \begin{eqnarray} {\bf E}({\bf r}) = \frac{1}{4\pi \epsilon_0} \frac{Q_1}{\left| {\bf r}_2 - {\bf r}_1 \right|^2} \frac{ {\bf r}_2 - {\bf r}_1 }{\left| {\bf r}_2 - {\bf r}_1 \right|}\ \ \ \ \ \ \ \ \ (7) \end{eqnarray} と表されるのである。式(7)で電場の直交座標系におけるベクトル表記を得ることができたが、この式からは\( x,\ y,\ z\)成分がどのくらいかはわかり難い。
そこで、最後に、式(7)を\(x,\ y,\ z\)成分に分けて表したいと思う。 電場ベクトルの\(x,\ y,\ z\)成分は、式(7)を\( {\bf r} = x {\bf e}_x + y {\bf e}_y + z {\bf e}_z \)であることと、 \( r = \sqrt{x^2 + y^2 + z^2} \)であることを使って、 \begin{eqnarray} E_x &=& \frac{Q_1}{4 \pi \epsilon_0} \frac{{(x_2 - x_1)}}{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}} {\bf e}_x \\ E_y &=& \frac{Q_1}{4 \pi \epsilon_0} \frac{{(y_2 - y_1)}}{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}} {\bf e}_y \\ E_z &=& \frac{Q_1}{4 \pi \epsilon_0} \frac{{(z_2 - z_1)}}{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}} {\bf e}_z \end{eqnarray} と表せるのである。この時、\(Q_1\)の座標を\( (x_1,\ y_1,\ z_1) \)、\(Q_2\)の座標を\( (x_2,\ y_2,\ z_2) \)として、\({\bf e}_x\)、\({\bf e}_y\)、\({\bf e}_z\)を\(x,\ y,\ z\)方向の単位ベクトルとした。