プラズマ振動の群速度（分散関係）

もしプラズマの運動に熱運動を考慮しない場合、プラズマ振動の周波数であるプラズマ周波数は以下のようになる。

\begin{eqnarray} \omega_p = \left( \frac{n_e e^2}{\epsilon_0 m_e} \right)^{1/2} \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

\begin{eqnarray} \omega = \left( \omega_p^2 + \frac{3k_B T_e}{m_e} k^2\right)^{1/2} \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

では初めにこの2つのプラズマ周波数を見ていこうと思う。熱速度を考慮せずに導出したプラズマ周波数は波数\( k \)の関数になっていないので、\( d\omega / dk \)で求められる群速度\( v_g \)は0となる。つまり、熱運動を考慮しない場合、プラズマ振動は伝搬しないのである。

次に、式(2)で表される熱運動を考慮して求めたブラズマ周波数を見てみる。式(2)の\( \omega \)は波数\( k \)の関数となっているため群速度は有限の値を持ち、振動は伝搬する。図1にプラズマ振動の分散関係を示す。

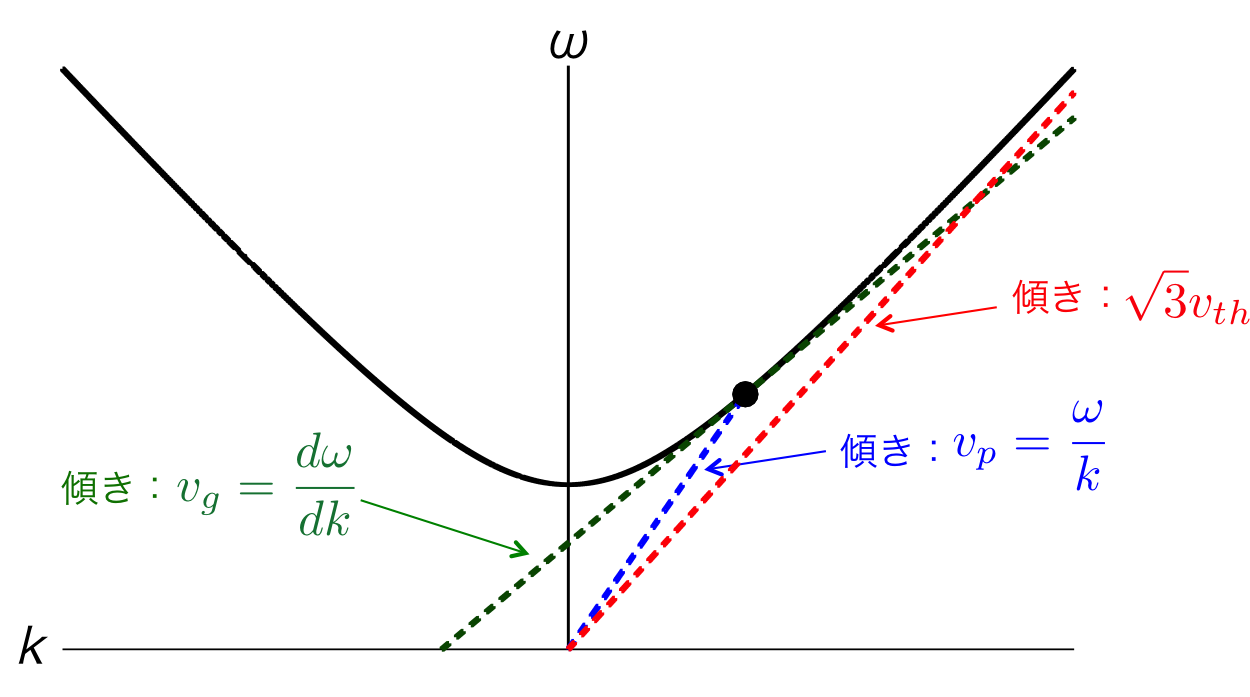
図1. プラズマ振動の分散関係

式(2)から群速度を求めると以下のようになる。

\begin{eqnarray} \frac{d \omega}{dk} = \frac{3 v_{th}^2}{v_p} \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

ここで、\( v_p\)は位相速度で\( \omega / k \)で表される。 \( v_{th} \)は1次元の熱速度で

\begin{eqnarray} v_{th} = \sqrt{ \frac{k_B T_e}{m_e} } \end{eqnarray}

となる。右辺、分子の3は1次元しか考えていない場合で、波の進行方向以外とエネルギーのやりとりをしないことを示したものである（ここでは詳しく説明しない）。

ある周波数と波数における群速度、位相速度、熱速度の関係は図1の緑、青、赤の点線で示している。群速度はある点での分散関係の接線となる。位相速度はある点と原点を結んだ直線となる。熱速度は分散関係の漸近線となるのである。

この3つの速度の比較を行う際には図1のようにそれぞれの速度の大きさを比較するとわかりやすい。大きな波数（小さい波長）ではほぼ熱速度と群速度が等しくなるので、ほぼ熱速度で擾乱が伝わる。小さい波数（大きな波長）では位相速度が熱速度よりも大きくなるが、群速度は遅いので、ゆっくりと擾乱が伝わるのである。