分極電流が作る分極電荷

プラズマは時間的に変化する電場の中では、電子（負電荷）とイオン（正電荷）が異なる方向にドリフトし、分極電流が流れるのであった。ここでは、その分極電流が分極電荷を生むことを示す。

図1に示すように分極した物質を考える。

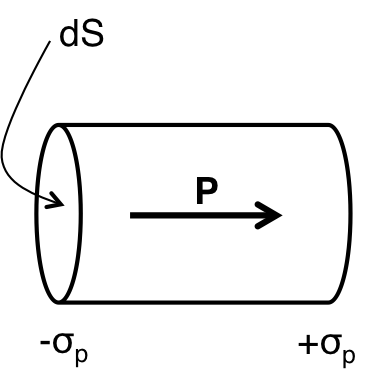
図1.　分極した物質

\( {\bf P} \)で分極した物質は物質の端に電荷\(\pm \sigma_p\)を貯める。ここで、\(\pm \sigma_p\)は面密度を示すことに注意する。 \( \pm \sigma_p \)の大きさは

\begin{eqnarray} \pm \sigma_p = \pm {\bf P} \cdot {\bf n}\ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

ここで、\( {\bf n} \)は微小断面積\( dS \)に垂直な単位ベクトルである。（図1では簡単のために分極ベクトル\( {\bf P} \)と並行である場合を書いている）

もし、分極が\( {\bf P} \)から\( {\bf P} + d{\bf P} \)に変化したとすると、端の電荷の面密度の絶対値は\( \sigma_p = \sigma_p + d\sigma_p \)となる。ここで、\( d\sigma_p = d{\bf P} \cdot {\bf n} \)である。この分極が時間変化してことによって、図1に示した物質の端を移動する電荷は

\begin{eqnarray} ds d\sigma_p = d{\bf s} \cdot d{\bf P}\ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

となる。ここで、\( ds \)は微小面積を表しているが、\( d{\bf P} \)や\( d\sigma_p \)は時間変化を表していることに注意すると

\begin{eqnarray} \frac{\partial \sigma_p}{\partial t} ds = \frac{\partial {\bf P}}{\partial t} \cdot d{\bf s}\ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

の関係を導くことができる。式(3)は分極が時間変化した際に微小区間\( ds \)に流れる電流を示している。このことから物質全体に流れる電流の密度\( {\bf j}\)は

\begin{eqnarray} {\bf j} \cdot d{\bf s} = \frac{\partial {\bf P}}{\partial t} \cdot d{\bf s}\ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

となり

\begin{eqnarray} {\bf j} = \frac{\partial {\bf P}}{\partial t}\ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}

の関係式が導ける。次に

\begin{eqnarray} \rho_p = \nabla \cdot {\bf P}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}

の関係式の両辺を時間微分することで、電流に関する連続の式

\begin{eqnarray} \frac{\partial \rho_p}{\partial t} + \nabla \cdot {\bf j}_p = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}

を導くことができる。この連続の式(7)から分極電流\( {\bf j}_p \)は分極電荷を生むことがわかる。