ベクトルの1次独立性と共面ベクトル
カテゴリー:物理数学
空間内で、図3-9に示すような四面体を作るベクトル\( {\bf A}, {\bf B}, {\bf C} \)がある時、この空間内のどのベクトルも
\begin{equation} {\bf r} = k {\bf A} + l {\bf B} + m {\bf C} \end{equation}
で表すことができる。
さらに、この表し方は一通りしか存在しない。
つまり、
\begin{equation}
k {\bf A} + l {\bf B} + m {\bf C} = k’ {\bf A} + l’ {\bf B} + m’ {\bf C}
\end{equation}
の時、
または、
である。
これが成り立つ場合、ベクトル\( {\bf A}, {\bf B}, {\bf C} \)は一次独立であると言う。
それぞれのベクトルが一次独立な場合、係数比較を行うことができる。
単位ベクトルも、それぞれ1次独立なベクトルである。
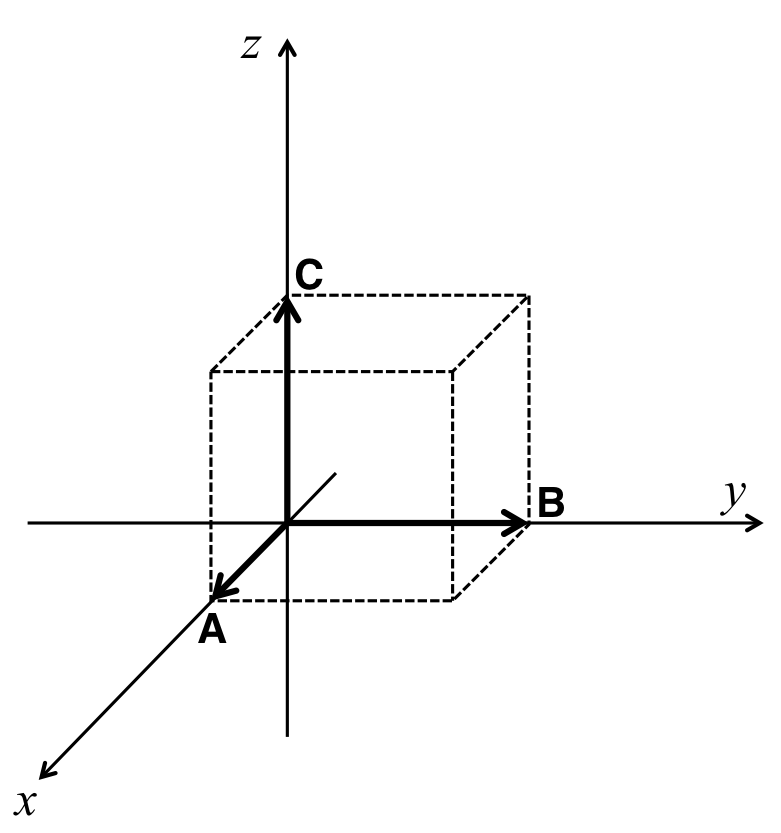
図3-9 1次独立なベクトル
逆に1次独立でないベクトルとは一体どんなものなのか?
答えは簡単で、互いに平行なベクトルである。
互いに平行なベクトル通しでは任意の点を表現することができない。
このように互いに平行なベクトルは互いに1次従属であると言う。
次に、図3-10のように点Pが直線上にない3点A, B, Cで決められる面上に存在する条件を考える。
点A, B, Cは直線上にないので、
\( \vec{AP} \)は
\begin{equation}
\vec{AP} = s\vec{AB} + t\vec{AC}
\end{equation}
と表すことができる。
\( \vec{OA}={\bf A}, \vec{OB}={\bf B}, \vec{OC}={\bf C}, \vec{OP}={\bf P} \)とすると、上のベクトル式は
\begin{equation} {\bf A} - {\bf P} = s ({\bf A}-{\bf B}) + t({\bf A} - {\bf C}) \end{equation}
と表すことができ、これを変形すると、
\begin{equation} {\bf P} = (1-s-t){\bf A} + s{\bf B} + t{\bf C} \end{equation}
となる。\( 1-s-t=r \)とすると、\( {\bf P} \)は
\begin{equation} {\bf P} = r{\bf A} + s{\bf B} + t{\bf C}, r+s+t=1 \end{equation}
という条件を満たすことがわかる。
これは点Pが直線上にない点A, B, Cでつくられる面上に存在するための条件であり、 共面条件と呼ばれる。
つまり共面条件は4点が同一平面上にある条件である。