単位ベクトルとベクトルの成分
カテゴリー:物理数学
大きさが1のベクトルを単位ベクトルと言う。
大きさが0でない任意のベクトル\( {\bf A} \)があるとすると、\( {\bf A} \)の単位ベクトルは \( {\bf A}/ | {\bf A} | \)で表すことができる。
多くの場合は直交座標の\( x, y, z \)方向それぞれの単位ベクトル\( {\bf i}, {\bf j}, {\bf k} \) を考える(図3-8)。
以下のような単位ベクトル\( {\bf i}, {\bf j}, {\bf k} \)を直交座標系\( x, y, z \)の基本ベクトルという。
\({\bf i}\):x軸と平行(+x向き)の向きの単位ベクトル
\({\bf j}\):y軸と平行(+y向き)の向きの単位ベクトル
\({\bf k}\):z軸と平行(+z向き)の向きの単位ベクトル
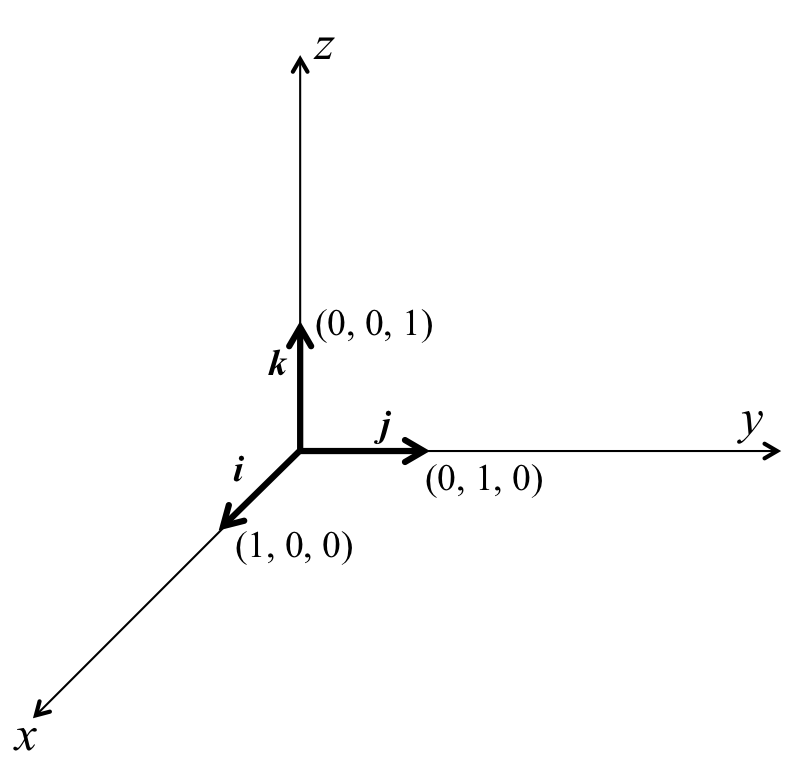
図3-8 直交単位ベクトル
単位ベクトルはベクトルの成分を表す時に便利である。
例えば、\( x \)軸方向に速度\( v_x \)で進んでいる物質の速度を、直交座標のベクトルで表すと
\begin{equation}
{\bf v} = v_x {\bf i}
\end{equation}
で表すことができる。
\( y, z \)軸にも速度を持っているなら
\begin{equation}
{\bf v} = v_x {\bf i} + v_y {\bf j} + v_z {\bf k}
\end{equation}
となる。
ここで、\( v_x, v_y, v_z \)はベクトル\( {\bf v} \)の\( x, y, z \)成分(ベクトルの成分)と呼ぶ。
ベクトルを成分で表すことは、ベクトルの特性を表すのに非常に便利である。
例えば、ベクトル\( {\bf A} \)は
\begin{equation}
{\bf A} = A_x {\bf i} + A_y {\bf j} + A_z {\bf k}
\end{equation}
と表すことができ(すでに\( {\bf v} \)で示した)、ベクトル\( {\bf A} \)の大きさは三平方の定理より、以下のように表すことができる。
\begin{equation} |{\bf A}| = \sqrt{ A^2_x + A^2_y + A^2_z } \end{equation}
足し算、引き算、掛け算のベクトル成分は以下のように表すことができる。
\begin{eqnarray} {\bf A} + {\bf B} &=& (A_x+B_x,\ A_y+B_y,\ A_z+B_z) \\ {\bf A} - {\bf B} &=& (A_x-B_x,\ A_y-B_y,\ A_z-B_z) \\ a{\bf A} &=& (aA_x,\ aA_y,\ aA_z) \end{eqnarray}
この成分は、直交座標のみならず、極座標、円柱座標でも同様にそれぞれの成分で表すことができる。
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/28f0c312.869b52e7.28f0c313.ac422153/?me_id=1213310&item_id=18449169&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F6188%2F9784046016188.jpg%3F_ex%3D240x240&s=240x240&t=picttext)
