微分方程式を用いた解法(RLC回路)
カテゴリー:物理数学
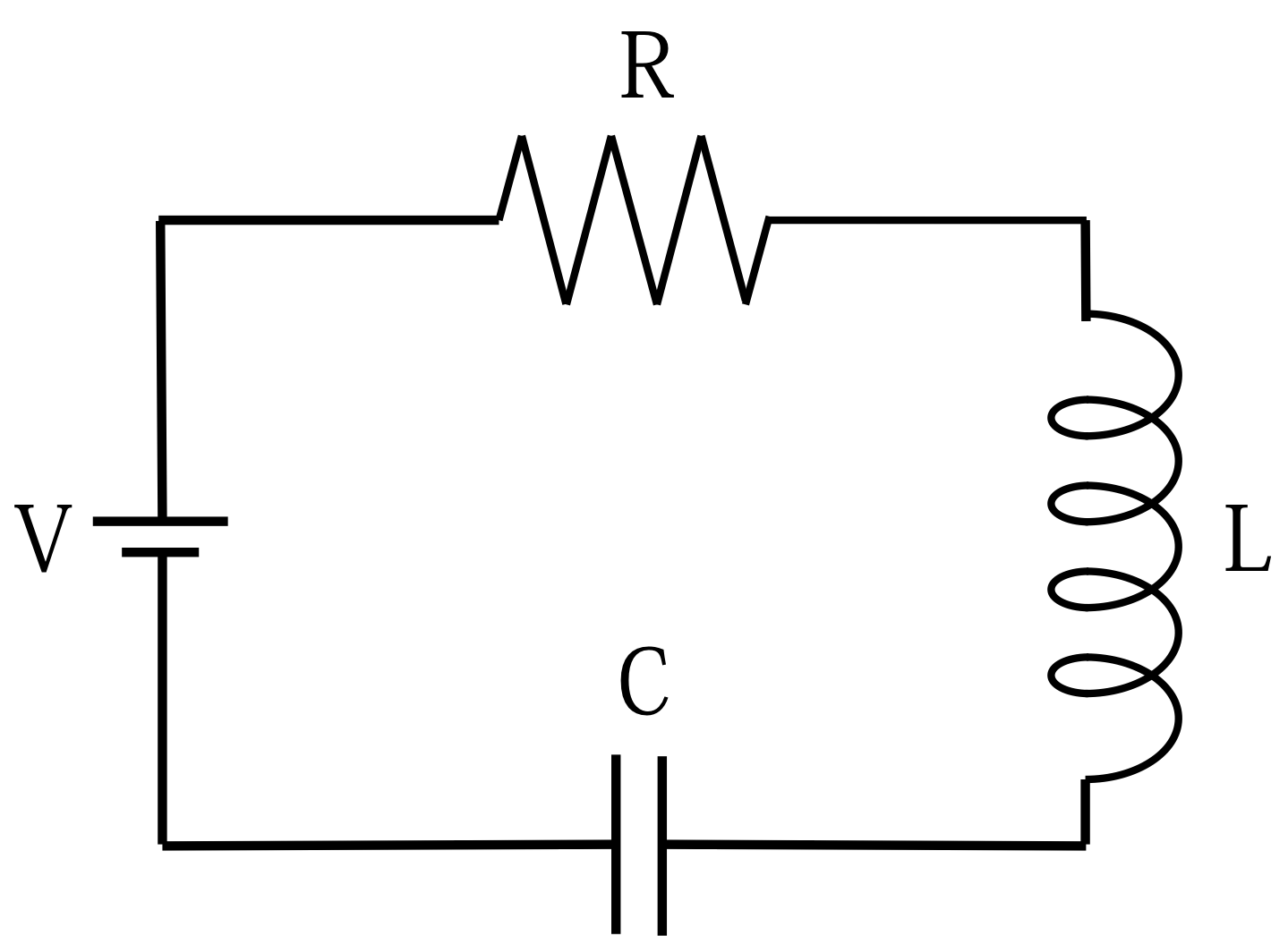
図1. RLC回路
図1のように抵抗R、コイルL、静電容量Cのコンデンサが直列に繋がれた回路を考える。
この回路はRLC回路と呼ばれる。
交流電源におけるRLC回路の特性を学ぶことは、電磁気学を学ぶ上で重要だが、ここでは直流電源の場合のみを考える。
RLC回路に電圧\( V \)の電池を接続すると、
キルヒホッフの法則より、
\begin{eqnarray} RI + L \frac{dI}{dt} + \frac{1}{C}\int I dt = V\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
となる。
ここで、\(R,\ L,\ C \)はそれぞれ電気抵抗、コイルのリアクタンス、コンデンサの電気容量、\( I \)は電流である。
式(1)を時間で微分するとよりシンプルに記述できて、
\begin{eqnarray} R \frac{dI}{dt} + L \frac{d^2I}{dt^2} + \frac{I}{C} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
となる。
式(2)の解が\( e^{\lambda t} \)で表されると仮定すると、特性方程式は
\begin{eqnarray} L \lambda^2 + R \lambda + \frac{1}{C} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3-1) \end{eqnarray}
となる。
書き直すと、
\begin{eqnarray} \lambda^2 + \frac{R}{L} \lambda + \frac{1}{LC} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3-2) \end{eqnarray}
となる。
\( \lambda \)は、解の公式から
\begin{eqnarray} \lambda = - \frac{R}{2L} \pm \sqrt{ \left( \frac{R}{2L} \right)^2 - \frac{1}{LC} } \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
であることがわかる。
つまり電流\( I \)は
\begin{eqnarray} I(t) &=& Ae^{ \left( - \frac{R}{2L} + \sqrt{ \left( \frac{R}{2L} \right)^2 - \frac{1}{LC} } \right) t } + Be^{ \left( - \frac{R}{2L} - \sqrt{ \left( \frac{R}{2L} \right)^2 - \frac{1}{LC} } \right) t } \\ &=& e^{ - \frac{R}{2L} t } \left\{ Ae^{ \left( \sqrt{ \left( \frac{R}{2L} \right)^2 - \frac{1}{LC} } \right) t} + Be^{ \left(- \sqrt{ \left( \frac{R}{2L} \right)^2 - \frac{1}{LC} } \right) t} \right\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
となる。
この解は減衰振動の形と同じである。
つまり、\( \left( R/2L \right)^2 \)と\( 1/LC \)のどちらかが大きいか、または等しいかで、電流の時間変化は変わる。
では、その電流の時間変化がどのようなものになるか図を使って説明していこうと思う。
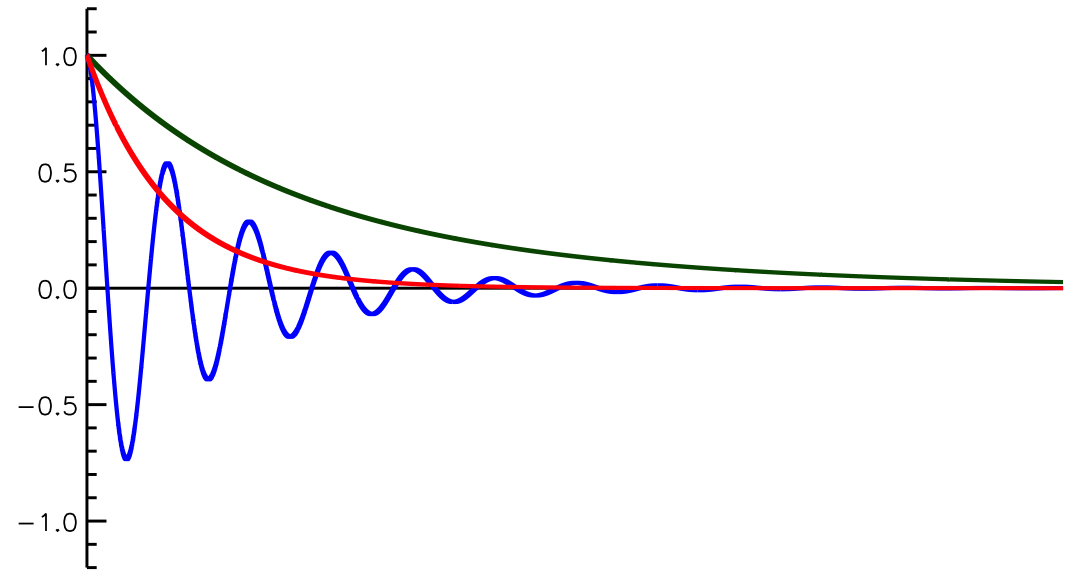
図2. 電流の時間変化。(緑)過減衰、(青)減衰振動、(赤)臨界減衰。
\( \left( R/2L \right)^2 > 1/LC \)の時
この場合、\( \sqrt{ \left( \frac{R}{2L} \right)^2 - \frac{1}{LC} } \)が実数となる。
すると、電流は時間とともに指数関数的に減衰していく。
これは図2の緑のラインに相当する。
\( \left( R/2L \right)^2 < 1/LC \)の時
この場合、\( e \)の肩が複素数となる。
つまり、式(5)はオイラーの公式により展開することができて、
\begin{eqnarray} I(t) = e^{ - \frac{R}{2L} t } \left( C_1 \cos \sqrt{ \left( \frac{1}{LC} - \frac{R}{2L} \right)^2 } t + C_2 \sin \sqrt{ \left( \frac{1}{LC} - \frac{R}{2L} \right)^2 } t \right) \end{eqnarray}
となり、振動をするのである。
ここで、\( C_1,\ C_2\)は定数。
このとき、電流の時間変化は図2の青線のように振幅を減衰させながら振動する。
この減衰量は
\begin{eqnarray} e^{ - \frac{R}{2L} t } \end{eqnarray}
で与えられる。
\( \left( R/2L \right)^2 = 1/LC \)の時
この場合、\( e \)の肩が0となる。
2階同次微分方程式の解き方を参考にして、
\begin{eqnarray} I(t) = e^{ - \frac{R}{2L} t } (A + Bt) \end{eqnarray}
となり、RLC回路で電流が最も早く減衰する。
これを臨界減衰と呼び、図2の赤線に相当する。