一定の力:地面との摩擦
カテゴリー:力学
なめらかな床に物体を置き、ゆっくりと押して手を離すと物体はある一定の速度で等速直線運動をする。
もし、この物体がなめらかな床を運動し続け、外部から力を加えられないのであれば、この物体は永遠に等速直線運動を続ける。
しかし、現実的にそれは難しく、一般的には摩擦や空気抵抗により、どんなに滑らかな床で物体を運動させてもいつかはその物体は静止してしまう。
まずは、物体に摩擦がかかるとどうなるのか見ていこうと思う。
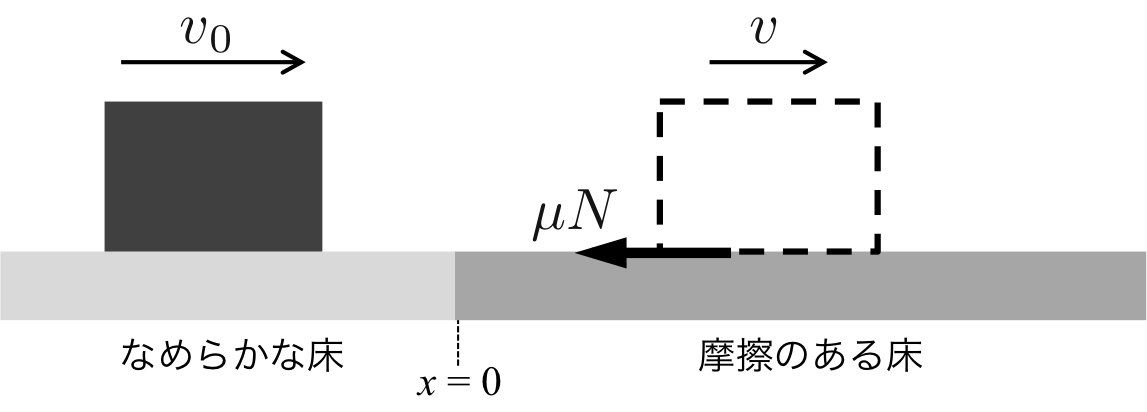
図1 なめらかな床から摩擦のある床に侵入する物体
図1のように、なめらかな床の上を速度\( v_0 \)で右側に等速直線運動をしている物体が、\( x=0 \)で摩擦のある床に侵入する場合を考える。 (ここで計算と考え方を簡単にするために、この物体の幅は考えないことにする。要するに、なめらかな床から摩擦のある床まで一瞬で切り替わるとする。)
摩擦のある床では、物体は垂直抗力\( N\)と動摩擦係数\( \mu \)を掛け合わせた力である摩擦力を受ける。
ニュートンの運動の法則から、この物体は摩擦のある床では左向きに力を受けることになる。
すると物体の速度は時間と共にどんどん落ちていき、やがて止まってしまうことがわかるだろう。
では運動方程式を解いて、摩擦によって、「いつ」、「どこで」止まるのかを計算していく。
止まる時
垂直抗力\( N \)は重力\( mg \)と釣り合っているので、\( N= mg \)である。
摩擦力\( \mu mg \)を、運動方程式の\( F \)に代入して、
\begin{eqnarray} m a = - \mu mg\ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
を得る。ここで、右向きを正としたので、摩擦力は負の値となる。加速度は速度の微分であるので、運動方程式は
\begin{eqnarray} m \frac{d v}{dt} = - \mu mg\ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
と書き直せる。式(2)を積分すると、
\begin{eqnarray} v = - \mu g t + v_0\ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
を得る。ここで、\( v_0 \)は初期条件である。
初期条件とは\( t=0 \)のときの、\( v \)の値である。
この場合は、摩擦のある床に侵入した瞬間を\( t=0 \)としているので、そのときの速度は\( v= v_0 \)とする。
さて、物体が止まる時の物体の速度は0となる。つまり、式(3)に\( v=0 \)を代入することで、
\begin{eqnarray} t = \frac{v_0}{\mu g}\ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
を得るのである。これで物体がいつ止まるのかを明らかにすることができた。
止まる位置
次に、どこで止まるのかを計算していく。
速度は位置の微分で表されるので、式(3)を次のように変換することができる。
\begin{eqnarray} \frac{d x}{dt} = - \mu g t + v_0\ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
この式を積分することで、
\begin{eqnarray} x = - \frac{1}{2} \mu g t^2 + v_0 t + x_0\ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
と位置の時間変化の式を得る。
ここで、\(x_0 \)は初期条件(積分定数)で、\( t=0 \)で\(x=0\)の原点にいることから\( x_0 = 0 \)であることがわかる。
この式(6)に止まるまでの時間、式(4)を代入することで、
\begin{equation} x = \frac{1}{2} \frac{v_0^2}{\mu g}\ \ \ \ \ \ \ \ \ \ (7) \end{equation}
と物体が止まるまでの距離がわかるのである。
このようにして、摩擦のように運動する向きと反対向きに力がかかる場合はその物体は必ず静止するのである。
ちなみに摩擦の場合は静止してしまうと、摩擦が働かなくなるので、物体は反対向きに動き出したりはしない。