フレネルの式

図1のように異なる媒質に光が入射するとき、入射光はどの程度反射してどの程度透過するのであろうか？

この、入射光、反射光、屈折光（透過光）の関係を表す式をフレネルの式と呼ぶ。

フレネルの式は以下のように表される。

\begin{eqnarray} t_p &=& \frac{2 n_A \cos \alpha}{n_B \cos \alpha + n_A \cos \beta} = \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)\cos(\alpha - \beta)} \\ r_p &=& \frac{n_B \cos \alpha - n_A \cos \beta}{n_B \cos \alpha + n_A \cos \beta} = \frac{\tan(\alpha - \beta)}{\tan(\alpha + \beta)} \\ t_s &=& \frac{2n_A \cos \alpha}{n_A \cos \alpha + n_B \cos \beta} = \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)} \\ r_s &=& \frac{n_A \cos \alpha - n_B \cos \beta}{n_A \cos \alpha + n_B \cos \beta} = - \frac{\sin(\alpha - \beta)}{\sin(\alpha + \beta)} \end{eqnarray}

フレネルの式に出てくる、\( t_p \)、\( t_s \)はそれぞれ、p偏光とs偏光の透過率である。

また、\( r_p \)、\( r_s \)はそれぞれ、p偏光とs偏光の反射率である。

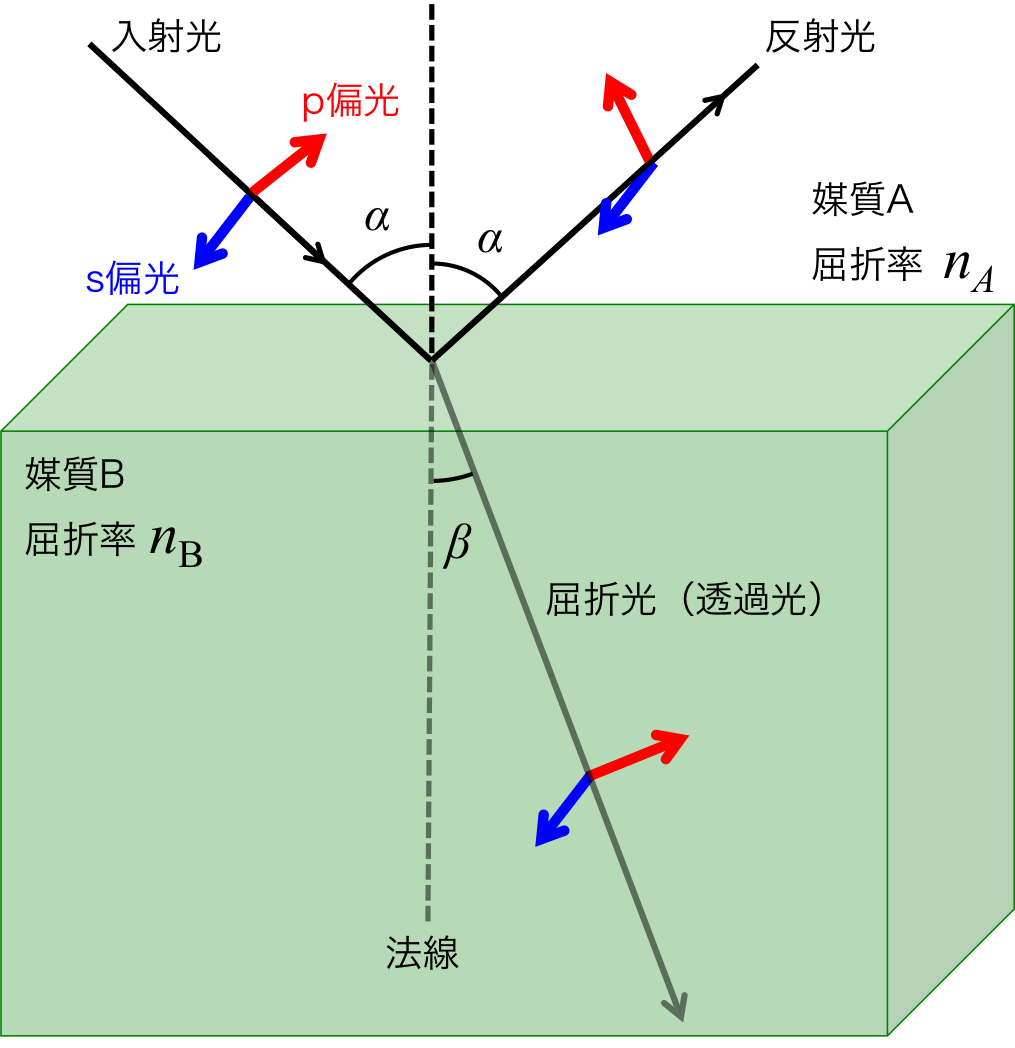
図1. 入射光の反射と屈折

フレネルの式を見て分かるように、入射光の偏光成分（p偏光とs偏光）によって透過率、反射率が異なるのである。

これは、フレネルの式が、それぞれの偏光方向において、電場・磁場の境界面に平行な成分が、境界面の両端で等しいという法則に基づいて導出されているからである。

これは境界条件と呼ばれる。

垂直な成分も境界条件で論じられることもあるが、とりあえずフレネルの法則の求め方を論じるには、上の１つだけで十分なので、垂直成分に関する境界条件は置いておこう。

この法則は一見すると難しそうに聞こえるが、行っていることは、

入射光 + 反射光 = 屈折光（透過光）

ということなのである。

では実際に境界条件を式に表すとどのようになるのか見ていこうと思う。

まずは、電場、磁場が境界面付近でどの向きで反射が起こるか確認する。（電束密度と磁束密度のベクトルは電場と磁場と同じ方向である。）

図2にその様子を示す。

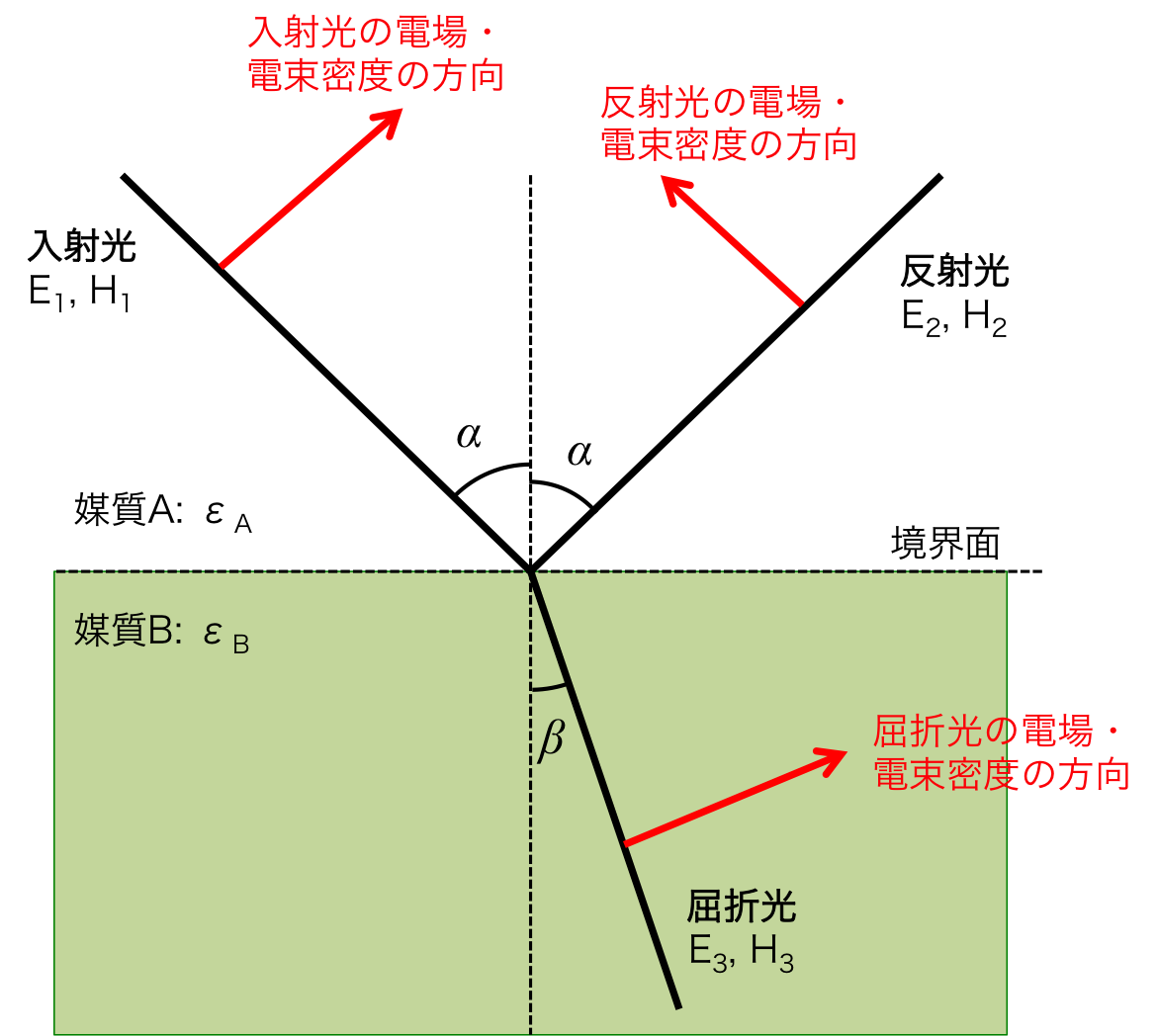
図2. 境界面付近での電場と電束密度の反射

図2は、実際には電場のベクトル（赤矢印）の原点（入射光が境界面に接する点）での様子であることに注意する。

さらに、図2はp偏光の場合を示している。 s偏光の場合は図2の電場が磁場に置き換わる。

以上のことに注意して、境界条件を求めてみる。

まず、p偏光の磁場成分は境界面に対して常に平行であるので、p偏光の磁場の入射光、反射光、屈折光の振幅を\( H_{P1},\ H_{P2},\ H_{P3} \)とすると単純に、
\begin{eqnarray} H_{P1} + H_{P2} = H_{P3}\ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

となる。

同様にして、s偏光の電場成分も、境界面に対して平行であるので、s偏光の電場の入射光、反射光、屈折光の振幅を\( E_{S1},\ E_{S2},\ E_{S3} \)とすると

\begin{eqnarray} E_{S1} + E_{S2} = E_{S3}\ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

と導ける。p偏光の電場成分とs偏光の磁場成分は境界面に対して水平な成分を持つ。

図2を見れば簡単に想像がつくと思うが、\( \cos \alpha \)または、\( \cos \beta \)を掛ければ良いだけである。

従って、式(1), 式(2)に加えて以下の方程式を求めることができる。

\begin{eqnarray} H_{S1}\cos\alpha - H_{S2}\cos \alpha &=& H_{S3} \cos \beta \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \\ E_{P1}\cos\alpha - E_{P2}\cos \alpha &=& E_{P3} \cos \beta \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

ここで、s偏光の磁場の入射光、反射光、屈折光の振幅を\( H_{S1},\ H_{S2},\ H_{S3} \)、p偏光の電場の入射光、反射光、屈折光の振幅を\( E_{P1},\ E_{P2},\ E_{P3} \)とした。

ここで、Maxwell方程式（マクスウェル方程式）から、

\begin{eqnarray} H = \sqrt{\frac{\epsilon}{\mu}} E \end{eqnarray}

の関係がある。\( \epsilon \)は誘電率で、\( \mu \)は透磁率である。

この関係を使って、(1), (3)式を書き直して、もう一度(2)、(4)式とまとめてみると、

\begin{eqnarray} \sqrt{\frac{\epsilon_A}{\mu_A}} E_{P1} + \sqrt{\frac{\epsilon_A}{\mu_A}} E_{P2} &=& \sqrt{\frac{\epsilon_B}{\mu_B}} E_{P3} \\ E_{S1} + E_{S2} &=& E_{S3} \\ \sqrt{\frac{\epsilon_A}{\mu_A}} E_{S1}\cos\alpha - \sqrt{\frac{\epsilon_A}{\mu_A}} E_{S2}\cos \alpha &=& \sqrt{\frac{\epsilon_B}{\mu_B}} E_{S3} \cos \beta \\ E_{P1}\cos\alpha - E_{P2}\cos \alpha &=& E_{P3} \cos \beta \end{eqnarray}

を得る。ここで、\( \epsilon_A \)、\( \epsilon_B \)、\( \mu_A \)、\( \mu_B \)は、それぞれ、媒質A、媒質Bでの誘電率と透磁率である。

媒質Aと媒質Bが磁性物質でないとすると、

\begin{eqnarray} \sqrt{\frac{\mu_A}{\mu_B}} \sim 1 \end{eqnarray}

と近似できる。なお、水や空気は磁性物質ではない。

この関係とスネルの法則から得られる

\begin{eqnarray} \frac{\sin \alpha}{\sin \beta} = \sqrt{ \frac{\epsilon_B}{\epsilon_A} } \end{eqnarray}

の関係を使うことで、フレネルの法則

\begin{eqnarray} t_p &=& \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)\cos(\alpha - \beta)} \\ r_p &=& \frac{\tan(\alpha - \beta)}{\tan(\alpha + \beta)} \\ t_s &=& \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)} \\ r_s &=& - \frac{\sin(\alpha - \beta)}{\sin(\alpha + \beta)} \end{eqnarray}

を導く事ができるのである。