無限に長い円柱(軸対象)に分布する電荷が作る電場
カテゴリー:電磁気学
図1に示すように無限に長い円柱に一様に分布している電荷が作る電場について考える。
この場合は円柱に沿った軸に対して、電荷は対象(軸対象)に分布しているため、軸方向に電場は生じない。

図1. 円柱状(軸対象)に分布する電荷が作る電場
つまり、図1のように軸に対して垂直な電場が生じる。 では、ガウスの法則を使って求めてみる。
ガウスの法則で電場を求める場合は、電荷を内部に含む閉曲面を考えなくてはならない。
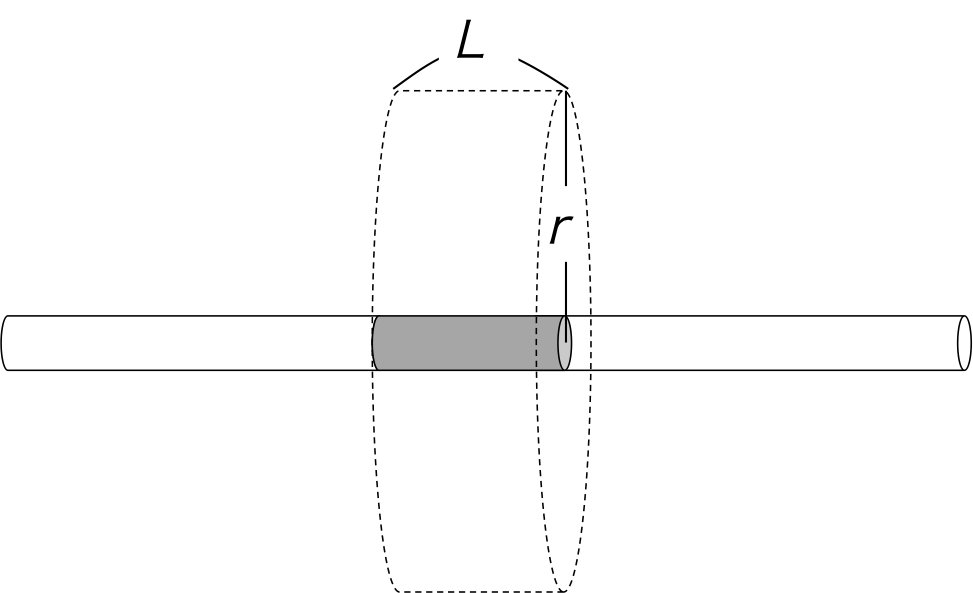
図2. ガウスの法則で電場を求めるための閉曲面
無限に長い円柱状に一様に分布している電荷が作る電場を求める場合には、図2に示すような閉曲面を考えるとわかりやすい。
この時、閉曲面の底面の半径は\( r \)、高さを\( L \)とする。
この場合、閉曲面の上面と下面(円のところ)は電場に対して平行であり、側面は電場に垂直である。 ここで、ガウスの法則は
\begin{eqnarray} \iint_S {\bf E} \cdot d{\bf A} = \frac{Q_{in}}{\epsilon_0} \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
で表される。 ここで、右辺の\( d{\bf A} \)は閉曲面の微小面積である。
この時、上で示したように上面と下面は電場に垂直なので、内積を取った時に消えるため、右辺は電場と側面の面積の掛け算であらわされる。 つまり、式(1)は
\begin{eqnarray} E 2\pi r L = \frac{Q_{in}}{\epsilon_0} \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
となる。\( Q_{in} \)は閉曲面内に存在する電荷量である。(図2の灰色の部分に存在する電荷である。)
電荷が存在する円柱の半径を\( R \)とすると、灰色の箇所の内部にある電荷\( Q_{in} \)は
\begin{eqnarray} Q_{in} = \pi R^2 L \rho \ \ \ \ \ \ \ \ (3) \end{eqnarray}
である。 ここで、\( \rho \)は電荷の密度である。式(3)を式(2)に代入することで、 この電荷が作る電場
\begin{eqnarray} E = \frac{R^2 \rho}{2 \epsilon_0 r} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
と求められる。この電場はもし閉曲面を円柱の外側に取った場合(\( r>R \))である。
つまり、閉曲面を円柱内部に取った場合(\( r < R \))の電場も求めなくてはならない。 もし、閉曲面を円柱の内部に取った場合、\( Q_{in} \)は
\begin{eqnarray} Q_{in} = \pi r^2 L \rho \ \ \ \ \ \ \ \ (5) \end{eqnarray}
となる。 この時電場は
\begin{eqnarray} E = \frac{r \rho}{2 \epsilon_0} \ \ \ \ \ \ \ \ (6) \end{eqnarray}
と求められる。 つまり、電場は、円柱からの距離によって異なり、
\begin{eqnarray} E =\left\{ \begin{array}{ll} \frac{R^2 \rho}{2 \epsilon_0 r} & (r>R) \\ \frac{r \rho}{2 \epsilon_0} & (r \le R) \end{array} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
と求められるのである。