ガウスの法則(積分形)
カテゴリー:電磁気学
ガウスの法則は電磁気学の中でも最も重要な法則の一つである。
また、ガウスの法則はどのような場合でも成り立つので、非常に便利な法則として知られている。
詳細にガウスの法則の求め方を述べる前に、まず初めにガウスの法則を以下に示す。
ガウスの法則式は、空間内にある電荷とその電荷が作る電気力線(電場)の関係式のことである。
\begin{eqnarray} \oint_S E\ dS= \frac{Q}{\epsilon_0}\ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
ここで\( E \)は電場、\( Q \)は閉局面\( S \)の内部に存在する電荷、\( \epsilon_0 \)は真空の誘電率である。
この式の意味するところは、風船のように途中で途切れず、また交差することのない閉曲面\( S \)における電気力線の数を足し合わせると、閉曲面内部に存在する電荷\( Q \)を\( \epsilon_0 \)で割った値と等しくなるのである。
この時、電気力線の本数は電場の大きさに比例するものとする。
なぜ、式(1)の左辺である電場を面積分すると閉曲面を貫く電気力線の本数となるのかは、曲面を貫く電気力線の本数のページを参照してもらいたい。
では、実際に式(1)を求めてみようと思う。
今、中心に電荷\( Q \)が置かれている半径\( r \)の球面を考える。
この時、球面上に電荷が作る電場は球面に対して垂直で、その大きさは
\begin{eqnarray} E_n = \frac{Q}{4 \pi \epsilon_0 r^2} \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
と表される(図1)。
ここで、\( {\bf n} \)は球面に対する法線ベクトルであり、正電荷の場合、法線ベクトルと電場の方向は一致する。
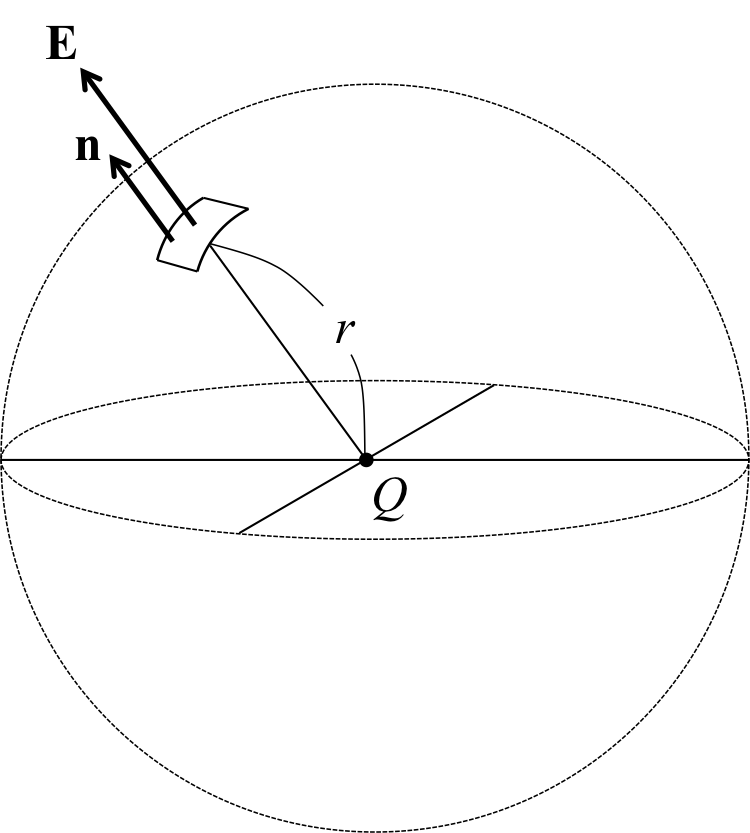
図1. 正電荷Qから出る電気力線と、閉曲面\(S_1\)と\(S_2\)である。
この時、半径\( r\)の球の表面積\( A = 4 \pi r^2 \)を垂直に貫く電気力線の本数は、
\begin{eqnarray} \Phi_E = \iint E_n\ dA \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
で表される。
なぜこの式で、球の表面を貫く電気力線の総数を表されるのかは、繰り返しになるが、曲面を貫く電気力線の本数のページを参照してもらいたい。
では、式(3)を解いていく。
式(3)は以下のように変形することができる。
\begin{eqnarray} \Phi_E = E_n \iint \ dA \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
ここに、式(2)を代入することで、
\begin{eqnarray} \Phi_E = \frac{Q}{4 \pi \epsilon_0 r^2} \iint \ dA \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
となる。
ここで、積分\( \iint \ dA \)は球の表面積を表すので、\( 4\pi r^2 \)となるのである。
つまり、式(3)は、
\begin{eqnarray} \Phi_E = \frac{Q}{\epsilon_0} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
と求めることができるのである。
まずは、この式の意味について考えていこうと思う。
式(6)には、球の半径\( r \)を含まない。
この事実は、電荷を中心とする球の表面の電気力線の数は、球の半径がどんなに大きくても、もしくはどんなに小さくても変わることがないということを意味する。
また、正電荷の場合、球の表面を\( Q/\epsilon_0\)の電気力線が外向きに貫き、負電荷の場合は球の表面を\( Q/\epsilon_0\)の電気力線が内側に貫いているのである。
言い換えると、「電場の大きさに比例するように電気力線を描くと、電気力線は正電荷から出て負電荷で消滅するが、途中で途切れたり、新たに発生することはない」ということを意味するのである。
つまり、
\( \Phi_E \) = 「閉曲面を内側から貫く電気力線の本数」
- 「閉曲面を外側から貫く電気力線の本数」
と言うことが言える。
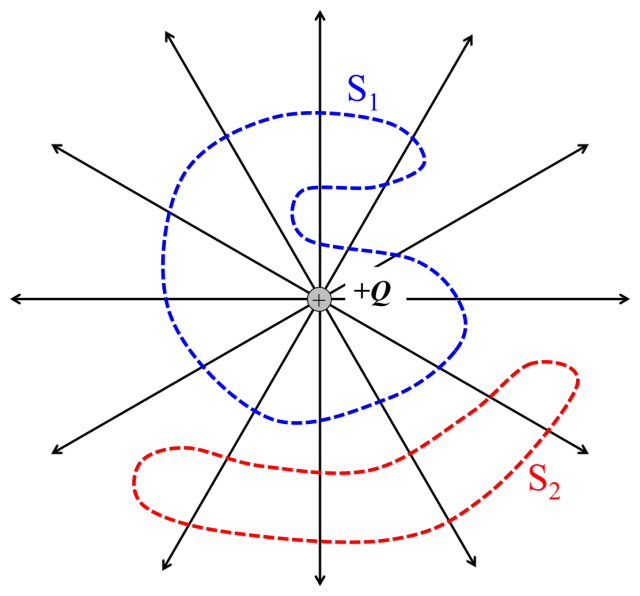
図2. 正電荷Qから出る電気力線と、閉曲面\(S_1\)と\(S_2\)である。
このことを念頭において、ガウスの法則の意味を考えてみたいと思う。
図2に示すような、正電荷\( Q \)を内側に含むような閉曲面\( S_1 \)と電荷を内側に含まない閉曲面\( S_2 \)を考える。
この図から見てわかるように、正電荷を含まない閉曲面\(S_2\)に侵入した電気力線は、必ず閉曲面の外側に出て行ってしまう。
つまり、トータルの電気力線(入っていく電気力線と出ていく電気力線の差)は0となる。
正電荷を内側に含む閉曲面\(S_1 \)は、出たり入ったりする電気力線はあるものの、内側から外側に貫く電気力線の本数の方が多い。
この時、閉曲面\( S_1 \)閉曲面のトータルの電気力線の本数は、\( Q/\epsilon_0 \)であることにはすぐに気づくだろう。
このことから以下の式が成り立つ。
\begin{eqnarray} \Phi_E &=& \iint_S E_n\ dA \\ &=& \left\{ \begin{array}{l} \frac{Q}{\epsilon_0} (閉曲面内部に正電荷Qがある時)\\ 0 (閉曲面内部に電荷がない時) \end{array} \right. \end{eqnarray}
この法則は1つの電荷のみを考えた法則であるので、より一般化するために複数の電荷の場合を考えなくてはならない。
といっても難しく考える必要はなく、電場の重ね合わせの原理を使えば簡単に複数の電荷の場合に一般化することができる。
複数の電荷\( Q_1,\ Q_2,\ Q_3, \cdots \)が作る電場\( {\bf E}\)は、各電荷が作る電場\( {\bf E}_1,\ {\bf E}_2,\ {\bf E}_3,\cdots\)の重ね合わせで表すことができる。
つまり、 \( {\bf E} = {\bf E}_1,\ {\bf E}_2,\ {\bf E}_3,\cdots \)と表されるのである。
この電場の中の閉曲面\( S \)を考えると、閉曲面を貫くトータルの電気力線(出ていく電気力線と入っていく電気力線の差、正味と言う)は、閉曲面\(S\)に内部にある電荷の総数、\( Q_1+\ Q_2+\ Q_3+ \cdots / \epsilon_0 \)で表されるのである。
つまり、\(i\)番目の電荷\( Q_i \)が作る電場を\( {\bf E}_i \)とすると、
\begin{eqnarray} \iint_S E_n= \iint_S \sum_i E_{in}\ dA = \sum_i \iint_S E_{in}\ dA =\frac{1}{\epsilon_0} \sum_i Q_i = \frac{Q_{in}}{\epsilon_0}\ \ \ \ \ \ \ \ (7) \end{eqnarray}
となる。
ここで、\( E_n\)は電場\( {\bf E} \)の閉曲面\( S \)の法線成分である。
また、\( Q_{in} \)は閉曲面\( S\)内部の電荷の総量である。
このことから以下のことが言える。
「閉曲面Sの内部から外部へ出る電気力線の正味の数」
= 「閉曲面内部の電荷の総数」/\( \epsilon_0 \)
となる。
これを式にすると、
\begin{eqnarray} \iint_S E_n\ dA = \iint_S {\bf E} \cdot d{\bf A} = \frac{Q_{in}}{\epsilon_0} \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
となる。
これをガウスの法則と呼ぶのである。
または、積分形のガウスの法則と呼ぶこともある。