自己相関関数

　もし時間的に変化する関数、\( x,\ y\)があったとする。 このとき、\(x,\ y\)がどの程度相関しているかということを考えるときは、\(x,\ y\)の値を、図1のように\( x-y\)平面状にプロットしてやればいい。

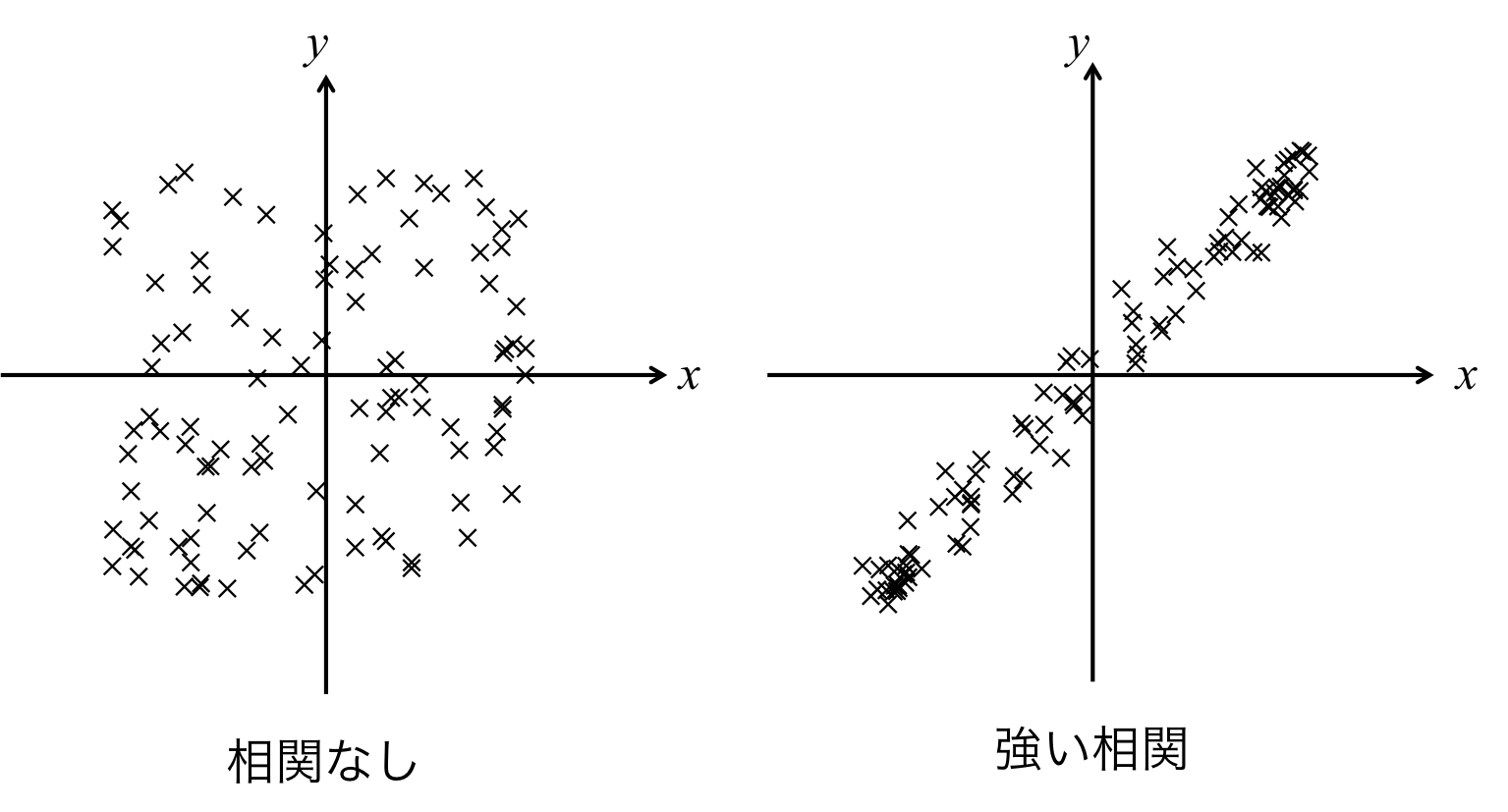
図1.

もし、\( x,\ y\)に全く相関がない場合は、\( x-y\)平面状に一様に点が打たれる。 その反対に、\(x,\ y\)がかなり似た変化、つまり強い相関を持つときは、一直線状にその点は密集する。 また、完全に\(x,\ y\)の値が一致している場合、点は直線上に打たれることになり、その傾きは1となる。 さらに、\(x\)が増えたときに\(y\)が減って、\( x\)が減った時に、\(y\)が増えるという逆の変化をしている時、傾きは-1となるのである。この場合は反相関という。
　このように\(x-y\)平面状に値を表示していけば、お互いにどの程度相関があるのかがわかる。 次に、相関とは式でどのように表されて行くのか見てみようと思う。 2つの関数の相関度は以下のように表される。 \begin{eqnarray} r_x &=& E\left[ \frac{y}{x} \right] = \frac{E[xy]}{E[x^2]} \\ r_y &=& E\left[ \frac{x}{y} \right] = \frac{E[xy]}{E[y^2]} \end{eqnarray} ここで、\( r_x \)はxに対する\(y\)の相関度、\(r_y \)は\(y\)に対する\(x\)の相関度である。 \(E\)はアンサンブル平均を意味する。 ここで、\(x\)と\(y\)を同じように扱うためには、 \begin{eqnarray} r = \frac{E[x,\ y]}{\sqrt{E[x^2]E[y^2]}}\ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} となる。この\(r\)の値が1に近ければ近いほど、\(x\)と\(y\)は相関があるという。 また、\(r\)の値が0に近ければ、\(x\)と\(y\)の相関は小さいということができるのである。 これは相関度と呼ばれる。 統計や信号処理などで使われる、自己相関というのは、自分自身とどの程度、時間的に相関があるのかを示す相関である。 つまり、自己相関とは\(x=y\)として、時間をずらして相関をとるのである。 自己相関については別のページで詳しく説明する。 広告