行列の積
行列の掛け算は足し算とは異なりかなり複雑になる。
まずは落ち着くために、行列の掛け算の中でも最も簡単な係数×行列の計算から示す。
\[
X \times
\left(
\begin{array}{ccc}
a & b & c \\
d & e & f \\
g & h & i
\end{array}
\right)
=
\left(
\begin{array}{ccc}
Xa & Xb & Xc \\
Xd & Xe & Xf \\
Xg & Xh & Xi
\end{array}
\right)
\ \ \ \ \ \ \ \ \ \ \ \ \ (4.3.1)
\]
行列と係数の掛け算は各成分に係数を掛け合わせればいいだけなのである。
では行列と行列の掛け算はどのように計算すれば良いのであろうか?
計算の例を見せる前に、行列の掛け算の定義を下に示す。

図4-3-1 行列の掛け算の定義
A行B列の列にはB行C列の行列しか掛け合わせることがでない。
つまり、右側の行列の「列」と左側の行列の「行」が一致しないとできない。
高校の数学の授業などではよく「行列の掛け算はしりとり」と言われる。
掛け合わされた後の解は左の行列の「行」と右側の行列の「列」を合わせた、A行D列の行列を得るのである。
では実際に最もシンプルな1行2列の行列と2行1列の行列の掛け算の例を示す。
このとき解は1行1列(普通の数字)の解が得られる。
\[
\left(
\begin{array}{cc}
a & b \\
\end{array}
\right)
\times
\left(
\begin{array}{c}
c \\
d \\
\end{array}
\right)
= ac + bd
\ \ \ \ \ \ \ \ \ \ \ \ \ (4.3.2)
\]
では2行2列の行列と2行1列の行列の計算はどうなるのであろうか?
その一例を示す。
\[
\left(
\begin{array}{cc}
a & b \\
c & d \\
\end{array}
\right)
\times
\left(
\begin{array}{c}
e \\
f \\
\end{array}
\right)
=
\left(
\begin{array}{c}
ae + bf \\
ce + df \\
\end{array}
\right)
\ \ \ \ \ \ \ \ \ \ \ \ \ (4.3.3)
\]
どのように計算されたかというと、
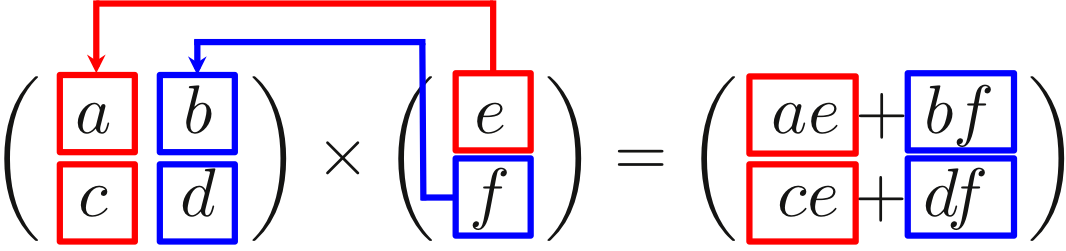
図4-3-2 行列の掛け算
というように計算されている。計算方法を言葉にしてみると、左側の行列の「1行1列目」と右側の行列の「1行1列目」を掛け合わせて、
左側の行列の「1行2列目」と右側の行列の「2行1列目」を掛け合わせたものを足し合わせて、解の1行1列目とする。
ということである。ここでも「しりとり」の法則は使えるが、何よりも行列の計算は回数をこなすことで計算の仕方を自然に覚えることができる。
(人間はこういう法則だった計算を覚えるのは比較的簡単なはず?)
では最後によくテスト等で出題される3行3列の行列の計算式を示す。
\[
\left(
\begin{array}{ccc}
A & B & C \\
D & E & F \\
G & H & I \\
\end{array}
\right)
\times
\left(
\begin{array}{ccc}
a & b & c \\
d & e & f \\
g & h & i \\
\end{array}
\right)
=
\left(
\begin{array}{ccc}
Aa + Bd + Cg & Ab + Be + Ch & Ac + Bf + Ci \\
Da + Ed + Fg & Db + Ee + Fh & Dc + Ef + Fi \\
Ga + Hd + Ig & Gb + He + Ih & Gc + Hf + Ii \\
\end{array}
\right)
\ \ \ \ \ \ \ \ \ \ \ \ \ (4.3.4)
\]
3行3列になると途端に解が煩雑になった。しかし、行列の計算はいくら行と列の数が増えても、
行列Aと行列Bの解のi行j列成分は、行列Aのi行目と行列Bのj列を掛け合わせて作られる
という法則は変わらない。つまり、式(4.3.2)の計算方法と、上の太字で示された法則を言っていればどんな行列の掛け算でも計算できるのである。
ちなみに、計算すればわかるが、行列\( A \)と行列\( B \)の掛け算、
\begin{eqnarray}
AB \ne BA\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4.5.3)
\end{eqnarray}
となり、通常の変数の掛け算とは異なり、行列\( A \)の左から行列\( B \)をかけるか、右から行列\( B \)を掛けるかで解は異なる。
広告

