複素数

\(a\)、\(b\)を実数として、\( i^2=-1 \)で表される虚数を使って、 \begin{equation} z = a + ib \end{equation} と表されるとき、\(z\)を複素数という。

このとき、\(a\)を実部（Real Part）、\(b\)を虚部（Imaginary Part）と呼ぶ。

物理では実部、虚部を分けて考えるために、 \begin{equation} z = \mathrm{Re}(z) + \mathrm{Im}(z) \end{equation} や、 \begin{equation} z = \mathfrak{Re}(z) + \mathfrak{Im}(z) \end{equation} として表される。

複素数を実部（横軸）と虚部（縦軸）に分けて座標系に表す。 すると、図1のようになる。

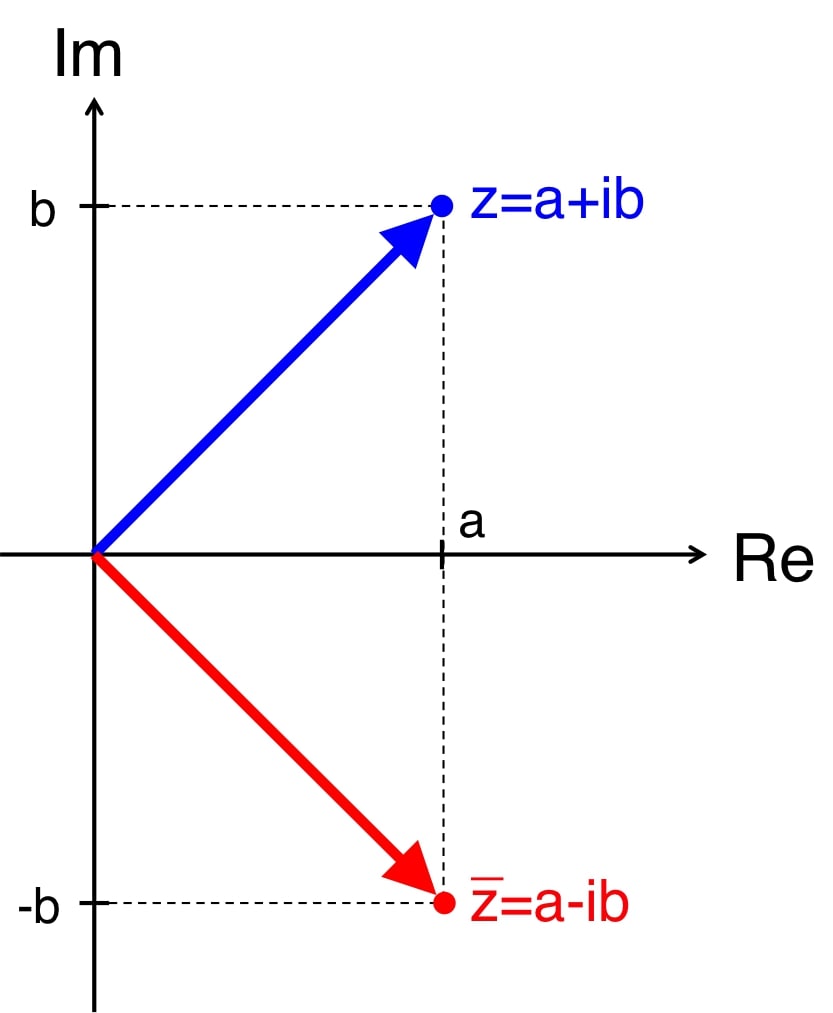
図1 自然対数と常用対数

このとき、実軸（横軸）に対して、線対称な赤の点を複素共役と呼ぶ。 \(z\)の複素共役は \begin{equation} \bar{z} = a - ib \end{equation} である。これを見てもわかるように、虚部にマイナスを掛けただけである。 複素数\( z \)とその複素共役\(\bar{z}\)は以下のような性質がある。 \begin{eqnarray} z + \bar{z} &=& 2\mathrm{Re}(z) \\ z - \bar{z} &=& 2 \mathrm{Im} (z) \\ z \bar{z} &=& |z|^2 \end{eqnarray}