相平面
調和振動の解は以下のように表されるのであった。 \begin{align} x &= A \cos \left( \omega_0 t + \alpha_0 \right) &(1) \\ \dot{x} = v &= - A \omega_0 \sin \left( \omega_0 t + \alpha_0 \right) &(2) \end{align} ではこれらの位置\( x\)と速度\( v\)から時間\( t\)を消す。 そのために式(1), (2)を以下のように変形する。 \begin{align} \cos \left( \omega_0 t + \alpha_0 \right) &= \frac{x}{A} &(3) \\ \sin \left( \omega_0 t + \alpha_0 \right) &= - \frac{v}{A \omega_0} &(4) \end{align} これらの式(3), (4)の両辺を二乗することで、\( \sin^2 \theta + \cos^2 \theta = 1\)の公式が使える。 すると、 \begin{eqnarray} \frac{x^2}{A^2} + \frac{v^2}{A^2 \omega^2_0}= 1\ \ \ \ \ \ \ \ (5) \end{eqnarray} を得ることができる。 この式を\(x-v\)平面にプロットしてみると、図1のような楕円を描く。 この楕円が描かれる\(x-v\)平面のことを相平面と呼ぶ。
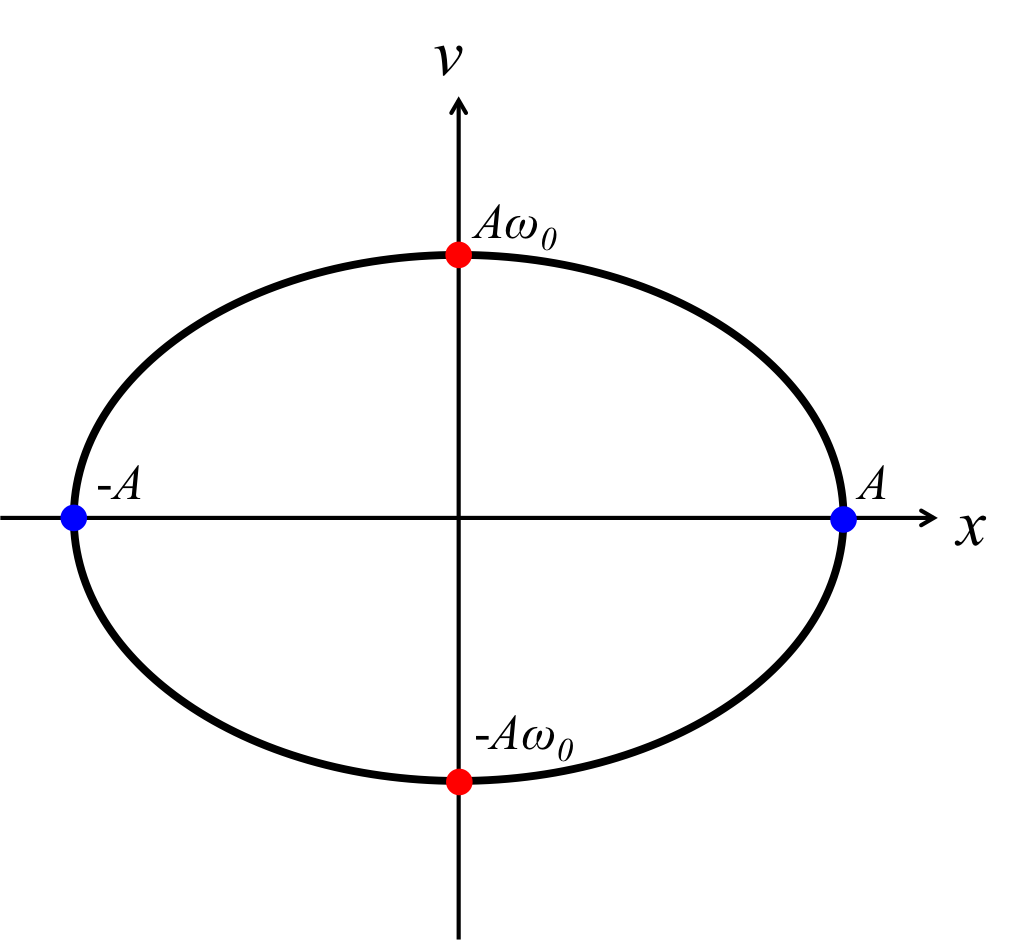
図1. 相平面
ではここで、ばねにつながれた質点の場合を考えてみよう。 右向きを正として、右方向にばねに取り付けられた質点を引っ張り、手をゆっくりと離す。 手を離した時間を\(t=0\)とすれば、\( t=0 \)で\( x = A \)、\( v = 0\)である。 その後、\(x\)の値は釣り合いの位置である\( x=0 \)に向かって行き、それに伴い左向き速度\(v\)は増加する。 釣り合いの位置\( x=0 \)で質点の速度は最大となり、その速度は\(- A \omega_0 \)である。 (ここで、右向きを正としたので、左向き速度は負になることに注意する。) その後、質点は釣り合いの位置を通り過ぎて\( x\)が負の領域に突入する、すると今度は速度が\( x=-A \)の位置で0となる。 再び質点は釣り合いの位置に向かい、そこで右向き最大の速度\( v = A \omega_0 \)を取るのである。 これらの一連の流れを見ると、まず初めに\(x\)軸正の青点から出発し、\( v= - A \omega_0 \)の赤点を通過し、\( x=-A \)の青点を通過する。 その後、\( v = A\omega_0\)を通過して、再び初期位相である青点に戻ってくる。 この一連の流れから質点の軌道が楕円を描き、時計周りに回ることがわかるだろう。 もちろん、この楕円を1週する時間\(T\)は、 \begin{eqnarray} T = \frac{2\pi}{\omega_0}\ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} である。位置と速度の初期位相がどのような状況でも質点は必ずこの楕円状に存在するのである。 (x=0で初速度を与えずに手を離すと全く動かず、調和振動をしないのでそれは例外)
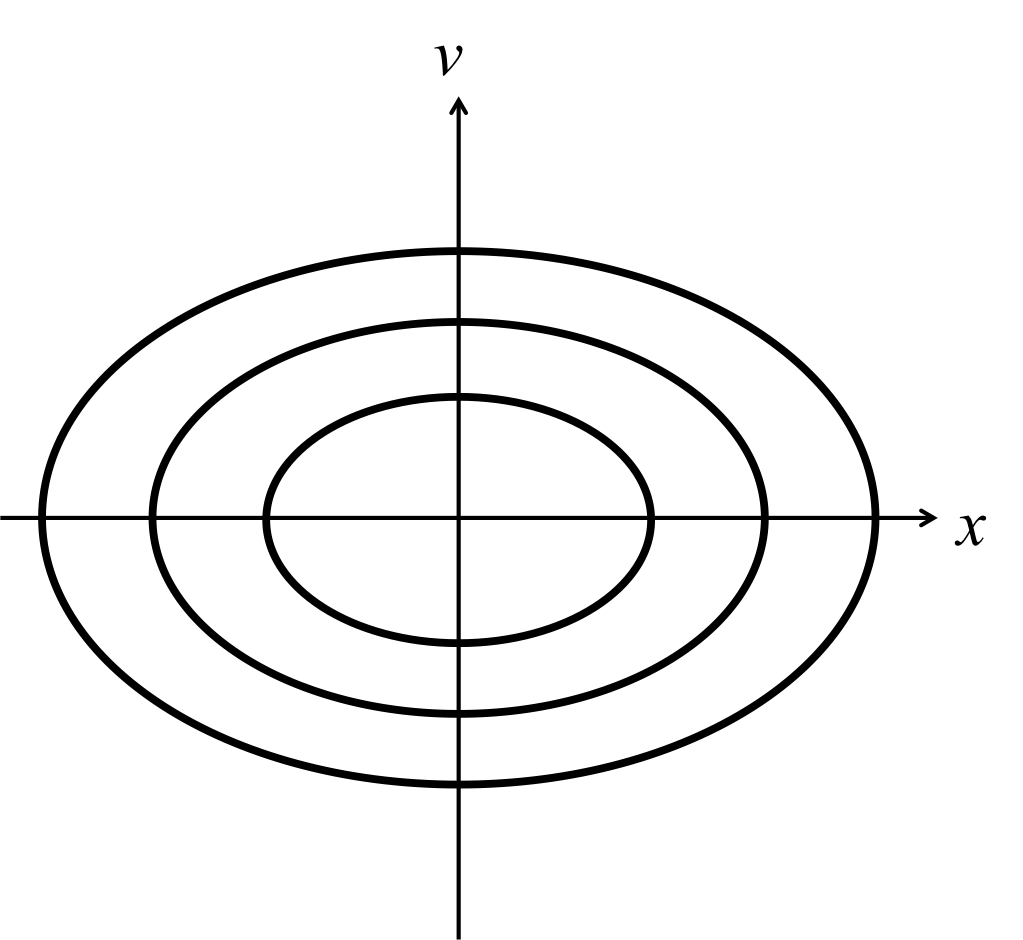
図2. 色々な初期移送における相平面
広告