　調和振動子の力学的エネルギー：振り子

　図1のような振り子（単振り子）の力学的エネルギーを導出する。力学的エネルギー\( E \)は、運動エネルギー\( T \)とポテンシャルエネルギー\( U \)を使って、 \begin{eqnarray} E = U + T \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} と表されるのである。

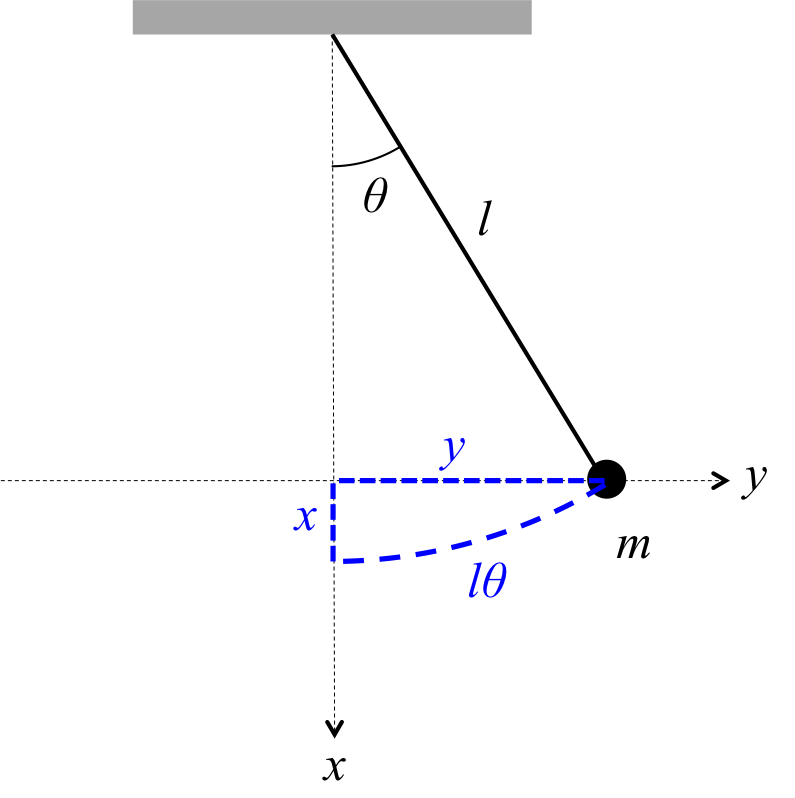
図1.　振り子

　ではまず、ポテンシャルエネルギーから求めていく。ポテンシャルエネルギーはこの場合、重力による位置エネルギーであるので、 \begin{eqnarray} U = mgl (1 - \cos\theta )\ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} で表される。この時、\(　\cos \theta \)をテイラー展開すると、 \begin{eqnarray} \cos \theta \sim 1 - \frac{\theta^2}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} となる。ここで、\( \theta \)は非常に小さいとして、3次以降を無視した。これを式(2)に代入すると、 \begin{eqnarray} U = \frac{1}{2}mgl \theta^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} を得る。
　ここで、図1の青で示した所に着目する。質点の位置は\( x,\ y\)で、再下点からの円弧の長さは\( l \theta \)である。もし、\( \theta \)が非常に小さいならば、この円弧は直線と近似することができて、三平方の定理で\( x \)と\( y \)を使って以下のように表すことができる。 \begin{eqnarray} x^2 + y^2 = l^2 \theta ^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} よって、ポテンシャルエネルギーは次のように書き換えることができるのである。 \begin{eqnarray} U = \frac{1}{2} \frac{mg}{l} (x^2 + y^2)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} 運動エネルギーは簡単に、 \begin{eqnarray} T = \frac{1}{2} m (\dot{x}^2 + \dot{y}^2)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray} と表されるので、力学的エネルギー\( E \)は、 \begin{eqnarray} E = \frac{1}{2} m (\dot{x}^2 + \dot{y}^2) + \frac{1}{2} \frac{mg}{l} (x^2 + y^2)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray} と求めることができるのである。
　ここで、式(8)を見てみると、\(x\)方向と\(y\)方向のエネルギーに分けられることが分かる。まず、\( x \)方向の力学的エネルギーを\( E_x \)としてみて、計算を進めてみる。 \begin{eqnarray} E_x = \frac{1}{2} m \dot{x}^2 + \frac{1}{2} \frac{mg}{l} x^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray} ここで、 \begin{eqnarray} x = A \cos ( \omega_0 t + \alpha_0 ) \ \ \ \ \ \ \ \ \ \ \ \ (10) \end{eqnarray} と置いて、これを式(9)に代入をする。ここで、\( \omega_0 = \sqrt{g/l}\)は角運動量、\( \alpha_0 \)は初期位相である。どうしてこのように置けるのかは、「調和振動が持つ解」のページを参照して欲しい。もちろん、\( x\)の1階微分は、 \begin{eqnarray} \dot{x} = - A \omega_0 \sin ( \omega_0 t + \alpha_0 ) \ \ \ \ \ \ \ \ \ \ \ \ (11) \end{eqnarray} である。これを式(9)に代入すると、 \begin{eqnarray} E_x &=& \frac{1}{2} m \omega_0^2 A^2 \sin^2 (\omega_0t + \alpha_0) + \frac{1}{2} \frac{mg}{l} A^2 \cos^2 ( \omega_0 t + \alpha_0 ) \\ &=& \frac{1}{2} \frac{mg}{l} A^2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \end{eqnarray} である。これを、ばねにつながれた質点の調和振動の力学的エネルギー、 \begin{eqnarray} E = \frac{1}{2} k A^2 = \frac{1}{2} m \omega_0^2 A^2\ \ \ \ \ \ \ \ \ (13) \end{eqnarray} と比べると、全く同じ値が得られていることがわかる。つまり、調和振動の場合は固有周期とその振動の振幅を使って、\( \frac{1}{2} m \omega_0 A^2 \)で力学的エネルギーが表されることがわかる。しかし、これはある条件が着く。先ほどの振り子の力学的エネルギーを求める際にまずは\( x\)方向のみの力学的エネルギーを求めた。 \( y\)方向の力学的エネルギーも存在し、その値は、 \begin{eqnarray} E_y = \frac{1}{2} \frac{mg}{l} B^2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14) \end{eqnarray} となる。\( B \)は式(12)を\( y\)方向に適応した際の振幅である。（\( x\)方向と\( y\)方向の振幅は異なる。）つまり、振り子の力学的エネルギーは、 \begin{eqnarray} E = \frac{1}{2}m\omega_0^2 \left( A^2 + B^2 \right) = \frac{1}{2}\frac{mg}{l} \left( A^2 + B^2 \right) \ \ \ \ \ \ \ (15) \end{eqnarray} となるのである。見てわかるように\( x\)方向のみで導出されたエネルギーより大きくなる。ばねによる調和振動は1次元で表されたが、振り子のように運動が\( x\)方向だけでなく\( y\)方向と言った2次元の場合もある。このように運動する次元が増えることを「自由度が増える」と言うのである。単純に次元が増えればその自由度でのエネルギーが全体のエネルギーに足し合わせるので、一般的にエネルギーは自由度が増すに従って増加する。自由度によってエネルギーが増えていく性質は、物理を勉強していく上で様々なところで顔を出し、最も有名なのが粒子の平均運動エネルギーである。

広告