Constant force: friction against the ground
When you push an object on a smooth floor, the object moves in uniform linear motion at a constant velocity. If no external force applied to the object, it would keep on moving in constant velocity forever. Generally, no matter how smooth the floor, an object stops sooner or later due to the friction from the air and floor. First, let's see what happens when friction acts on the object.
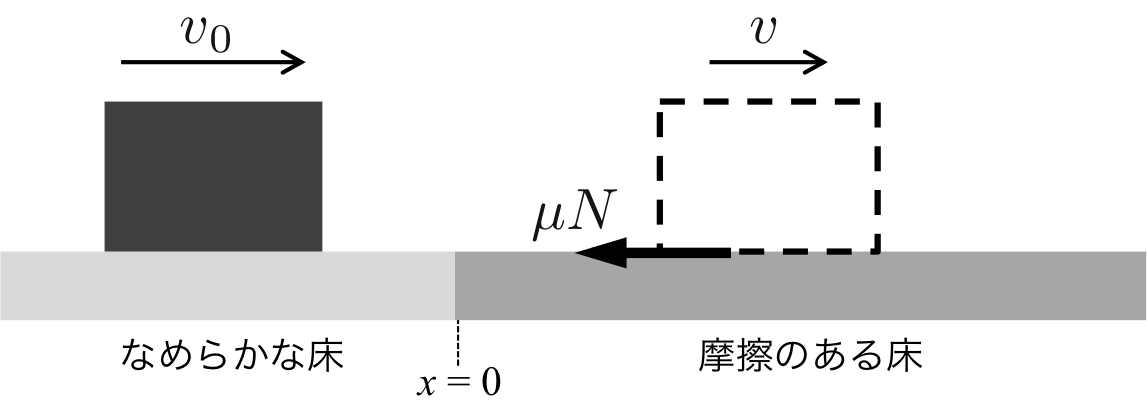
Figure 1 An object which move into the frictional floor from smooth floor
As shown in Figure 1, we consider an object moving in uniform linear motion at a velocity of \( v_0 \) in rightward on the smooth floor and it gets into the frictional floor at the position of \( x=0 \). (To simplify, we assume that the object has not width, so the object gets into a floor with friction in an instant.)
On a floor with friction, the friction force which subjects to the object is equal to the friction coefficient of kinetic friction \( \mu \) times the normal force \( N\). According to Newton's law of motion; the friction force opposes the motion of the object. Which means that the direction of the frictional force is leftward in this case. Then the object velocity gradually decelerates with time, and the object eventually stops.
So, let's solve when and where the object stops due to friction by using the equation of motion. We know the normal force \( N \) balance with the gravity \( mg \), so \( N= mg \). Substituting \( \mu mg \), which is the friction force subject to the object, into \( F \) in the equation of motion and obtains the following equation.
\begin{eqnarray}
m a = - \mu mg\ \ \ \ \ \ \ \ \ \ (1)
\end{eqnarray}
Here, we set the rightward direction as positive, so the friction force has a negative value. Since acceleration is a derivative of velocity, the equation of motion is rewritten as below.
\begin{eqnarray}
m \frac{d v}{dt} = - \mu mg\ \ \ \ \ \ \ \ \ \ (2)
\end{eqnarray}
Integrate Equation (2) to obtain Equation (3).
\begin{eqnarray}
v = - \mu g t + v_0\ \ \ \ \ \ \ \ \ \ (3)
\end{eqnarray}
where \( v_0 \) is an initial velocity. The initial velocity is the value of \( v \) when \( t=0 \). In this case, we assumed the moment in which the object gets into the floor with friction as \( t=0 \), so the velocity is \( v= v_0 \). When the object stops, the velocity becomes 0.
Substituting \( v=0 \) into Equation (3) obtains the following equation.
\begin{eqnarray}
t = \frac{v_0}{\mu g}\ \ \ \ \ \ \ \ \ \ (4)
\end{eqnarray}
We reveals the time when the object stops. Next, we are going to calculate where the object stops. Since velocity is a derivative of position, Equation (3) is rewritten as below.
Integrating Equation (3), the equation of temporal change of position obtained as below.
\begin{eqnarray}
\frac{d x}{dt} = - \mu g t + v_0\ \ \ \ \ \ \ \ \ \ (5)
\end{eqnarray}
\begin{eqnarray}
x = - \frac{1}{2} \mu g t^2 + v_0 t + x_0\ \ \ \ \ \ \ \ \ \ (6)
\end{eqnarray}
where \(x_0 \) is the constant of integration indicating the initial position \( x=0\). Because the object located on the \( x=0\) at \( t=0 \), \( x_0 \) would be \( 0 \). Substituting Equation (4) expresses the time until the object stops into Equation (6) and obtains Equation (7).
\begin{equation}
x = \frac{1}{2} \frac{v_0^2}{\mu g}\ \ \ \ \ \ \ \ \ \ (7)
\end{equation}
Equation (7) express the stopping distance of the object. Like friction force, when a force is acting in the opposite direction of the motion, the object will always stop.
sponcered link
