正弦波とノイズの自己相関関数

　正弦波や余弦波の自己相関関数は余弦波となる。
これについて詳しく知りたい場合は、正弦波の自己相関関数と余弦波の自己相関関数のページを参照して欲しい。 通常は、綺麗な正弦波や余弦波を得られることはほぼない。 レーダーの信号や、周期的成分を含んだ観測データは図1のようにノイズを含めて計測される。

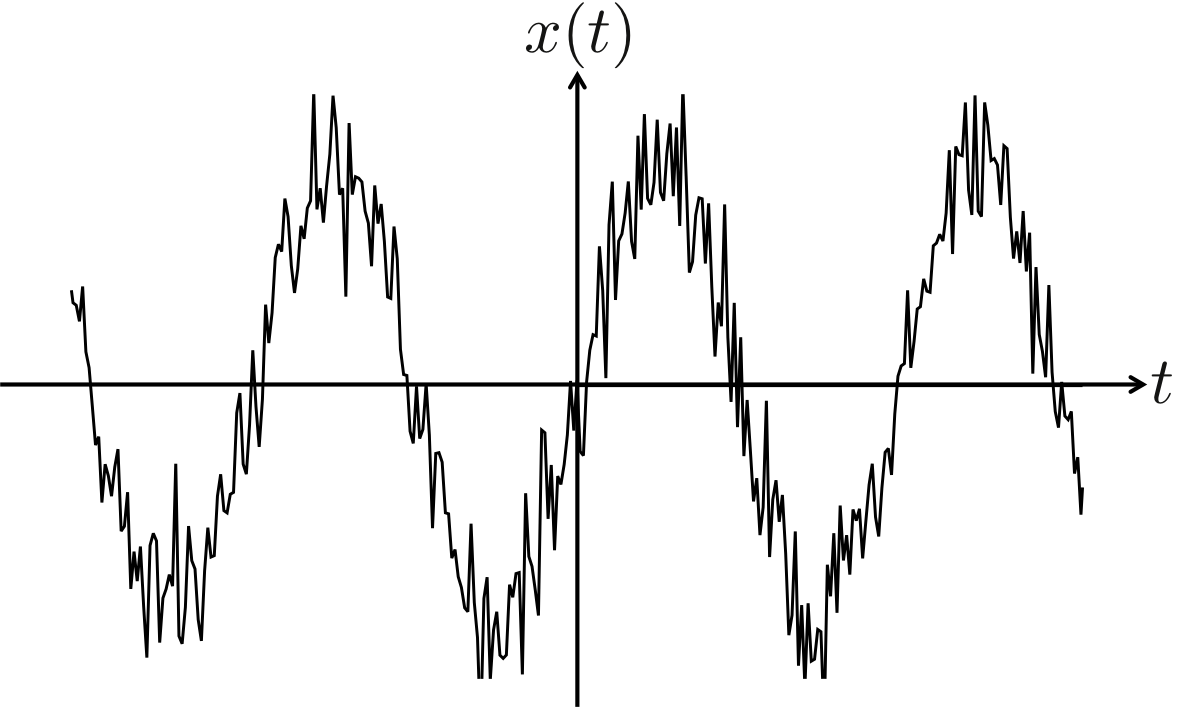
図1.

図1で表された正弦波にノイズ（雑音）が重なった関数\( x(t) \)は、 \begin{eqnarray} x(t) = a\sin (\omega t + \phi) + r(t)\ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} で表される。 ここで、\( r(t) \)はノイズを意味し、\( \phi \)は位相である。 \(x(t)\)に対して、\( \tau \)のラグを取った関数\( x(t+\tau) \)は、 \begin{eqnarray} x( t + \tau ) &=& a \sin(\omega (t+ \tau) + \phi) + r(t + \tau) \\ &=& a \sin(\omega t + \phi)\cos \omega \tau + a\cos (\omega t + \phi) \sin \omega \tau + r(t+ \tau)\ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} で表される。 自己相関関数を得るための\( x(t) x(t+\tau) \)は以下のようになる。 \begin{eqnarray} x(t)x(t+\tau) &=& a\sin^2 (\omega t + \phi)\cos \omega \tau + a\sin (\omega t + \phi) \\ & & + a r(t) \sin(\omega (t+\phi) +\phi)\\ & & + a r(t+\tau) \sin (\omega t + \phi) + r(t)r(t+\tau) \\ \\ &=& \frac{a^2}{2} \cos \omega \tau - \frac{a^2}{2} \cos (\omega(2t+\tau) + 2\phi) \\ & & + a r(t) \sin(\omega (t+\phi) +\phi)\\ & & + a r(t+\tau) \sin (\omega t + \phi) + r(t)r(t+\tau) \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} もし、式展開が不明な場合は正弦波の自己相関関数のページを参考にして欲しい。 式(3)のアンサンブル平均を取ったものが、自己相関関数\( C(\tau) \)となる。 式(3)のアンサンブル平均を取るためには、\( x(t) \)の第\( i \)番目の標本を \begin{eqnarray} x_i(t) = a\sin (\omega t + \phi_i) + r_i(t)\ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} としなければならない。 よって、自己相関関数は、 \begin{eqnarray} C(\tau) &=& E[\ x_i(t)x_i(t+\tau)\ ] \\ &=& \frac{a^2}{2} \cos \omega \tau + E[\ - \frac{a^2}{2} \cos (\omega(2t+\tau) 　　　　　　+ 2\phi_1)+ a r_i(t) \sin(\omega (t+\tau) +\phi_i) + a r_i(t+\tau) \sin (\omega t 　　　　　　 + \phi_i) + r_i(t)r_i(t+\tau) \ ]\ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) 　　　　\end{eqnarray} となるのである。 ここで、\( E \)はアンサンブル平均を意味する。 少し複雑な式ではあるが、意味は単純なので頑張って解いていく。 式(5)の中の \begin{eqnarray} C(\tau) &=& E[\ - \frac{a^2}{2} \cos (\omega(2t+\tau) + 2\phi_1)+ a r_i(t) \sin(\omega (t+\tau) +\phi_i) 　　　+ a r_i(t+\tau) \sin (\omega t + \phi_i) \ ] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} について考える。 三角関数の位相をずらした関数どうしの平均を取ると言う意味だが、平均を取る位相をずらした関数（標本）の数を増やせば増やすほどその平均（アンサンブル平均）は0に近づいていく。 今は無限個の標本に対するアンサンブル平均を取ることを考えている。 つまり、式(6)は0となるのである。 よって、正弦波とノイズの関数の自己相関関数は、 \begin{eqnarray} C(\tau) = \frac{a^2}{2} \cos \omega \tau + \psi(t) \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray} と表すことができるのである。 ここで、\( \psi(t) \)とは、ノイズの自己相関関数で、 \begin{eqnarray} \psi(t) = E[\ r_i(t)r_i (t+\tau) \ ] \end{eqnarray} となるのである。 理想的なノイズであっても必ず自己相関関数を持つ。 もし、ノイズが正弦波の振幅に対して大きい場合、式(7)で表される自己相関関数は第2項が大きくなってしまい、正弦波の自己相関関数である式(7)の第1項は埋もれてしまう。 よって、良い計測をするためにはできる限りノイズを小さくすることが求められるのである。

広告