正弦波の自己相関関数

　自己相関関数とは、自分自身と時間的にどの程度似ているかということを表す関数であった。 自己相関関数を学んだ時によく例として、正弦波や余弦波の自己相関関数と自己相関係数を求める。 ここでも、まず最も単純な例題として、正弦波の自己相関関数を求めてみる。
　正弦波（サイン波）は言うまでなく、 \begin{eqnarray} x(t) = a \cos ( \omega t + \phi)\ \ \ \ \ \ \ \ \ (1) \end{eqnarray} であり、直交座標で表すと図1のようになる。

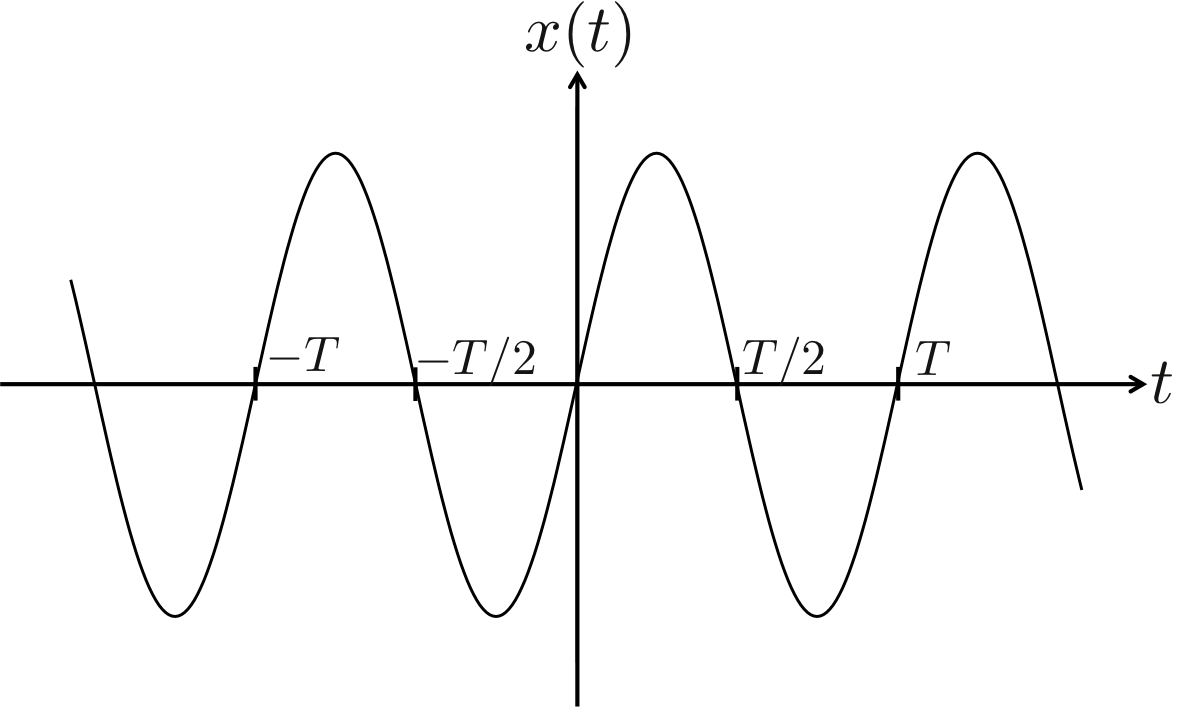
図1.

自己相関は\( x(t+\tau) \)として、\( \tau\)の値を変化させていきながら、\( x(t) \)と\( x(t + \tau) \)の相関を取るのであった。 まずは、図から想像してみると、\( \tau =0 \)の時は完全に重なるので、自己相関は最大となる。 \( \tau \)をどんどん大きくしていくと、\( \tau = T\)のところで再び自己相関が最大となる。 このように\( \tau = nT\ (n=\cdots, -2,\ -1,\ 0,\ 1,\ 2,\ 3, \cdots) \)となるところで自己相関が最大となることは容易に想像がつく。 これだけでは断定できないが、正弦波の自己相関関数は、余弦波\( \cos \omega t\)で変化すると予想ができる。
　では、実際に求めていこうと思う。\( x(t+ \tau ) \)は以下のように表される。 \begin{eqnarray} x( t + \tau ) &=& a \sin ( \omega(t + \tau) + \phi) \\ &=& a \sin (\omega t + \phi)\cos \omega t + a \cos (\omega t + \phi) \sin \omega t\ \ \ \ \ \ \ \ (2) \end{eqnarray} である。すると、\( x(t) x(t+\tau) \)は以下のようになる。 \begin{eqnarray} x(t) x(t + \tau) = a^2 \sin^2 (\omega t + \phi)\cos \omega \tau + a^2 \sin(\omega t + \phi) \cos (\omega t + \phi) \sin \omega \tau \ \ \ \ \ \ (3) \end{eqnarray} ちょっとこの式は複雑なので、三角関数の加法定理と倍角の公式を使ってもう少し整理する。 \begin{eqnarray} x(t) x(t+ \tau) &=& a^2 \frac{1 - \cos(2\omega t + 2 \phi)}{2} \cos \omega \tau \frac{a^2}{2} \sin (2 \omega t + 2\phi) \sin \omega \tau \\ &=& \frac{a^2}{2} \cos \omega \tau - \frac{a^2}{2} \left\{ \cos(2\omega t + 2\phi)\cos \omega \tau - \sin(2\omega t + 2\phi)\sin \omega \tau \right\} \\ &=& \frac{a^2}{2} \cos \omega \tau - \frac{a^2}{2} \cos (2\omega t + \omega \tau + 2 \phi) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} では、まずは自己相関関数よりも容易に求められる自己相関係数について求める。 まず、式(4)を0から\(nT\)まで積分する。 \begin{eqnarray} \int^{nT}_0 x(t)x(t+\tau) \ dt &=& \int^{nT}_0 \frac{a^2}{2} \left\{ \cos \omega \tau - \cos (2\omega t + 2 \phi + \omega \tau)\right\} \ dt \\ &=& \frac{nT a^2}{2} \cos \omega \tau \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} これを使って、自己相関係数\( R(\tau) \)は、 \begin{eqnarray} R(\tau) &=& \frac{\int^{nT}_0 x(t)x(t+\tau) \ dt }{\int^{nT}_0 x^2(t) \ dt } \\ &=& \cos \omega \tau \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} と求めることができる。
　次に、自己相関関数を得るために、\( x(t)x(t+\tau) \)のアンサンブル平均を取る。 アンサンブル平均を取るためには、第\(i\)番目の標本を、 \begin{eqnarray} x_i(t) x_i(t + \tau) = \frac{a^2}{2} \cos \omega \tau - \frac{a^2}{2} \cos (2\omega t + \omega \tau + 2 \phi_i)\ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray} としなければならない。つまり、正弦波の波形は同じであるが、位相が標本ごとにずれているのである。 以上より、正弦波の自己相関関数\( C(\tau) \)は、 \begin{eqnarray} C(\tau) &=& E [x_i (t) x_i (t + \tau)] \\ &=& \frac{a^2}{2} \cos \omega \tau - \frac{a^2}{2} E \left[ \cos (2\omega t + \omega \tau + 2 \phi_i) \right]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray} から求めることができる。 ここで、\( E\)はアンサンブル平均を意味する。 この時、第二項について考えて見る。これは、位相をずらした余弦波（\( \cos \)）について平均を取っていることを意味している。 今は、無限個の標本についての平均を取る場合を考えるので、この第二項は0になるのである。 つまり、正弦波の自己相関関数は、 \begin{eqnarray} C(\tau) = \frac{a^2}{2} \cos \omega \tau \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray} となるのである。やはり、予想した通り正弦波の自己相関関数は余弦波となるのである。

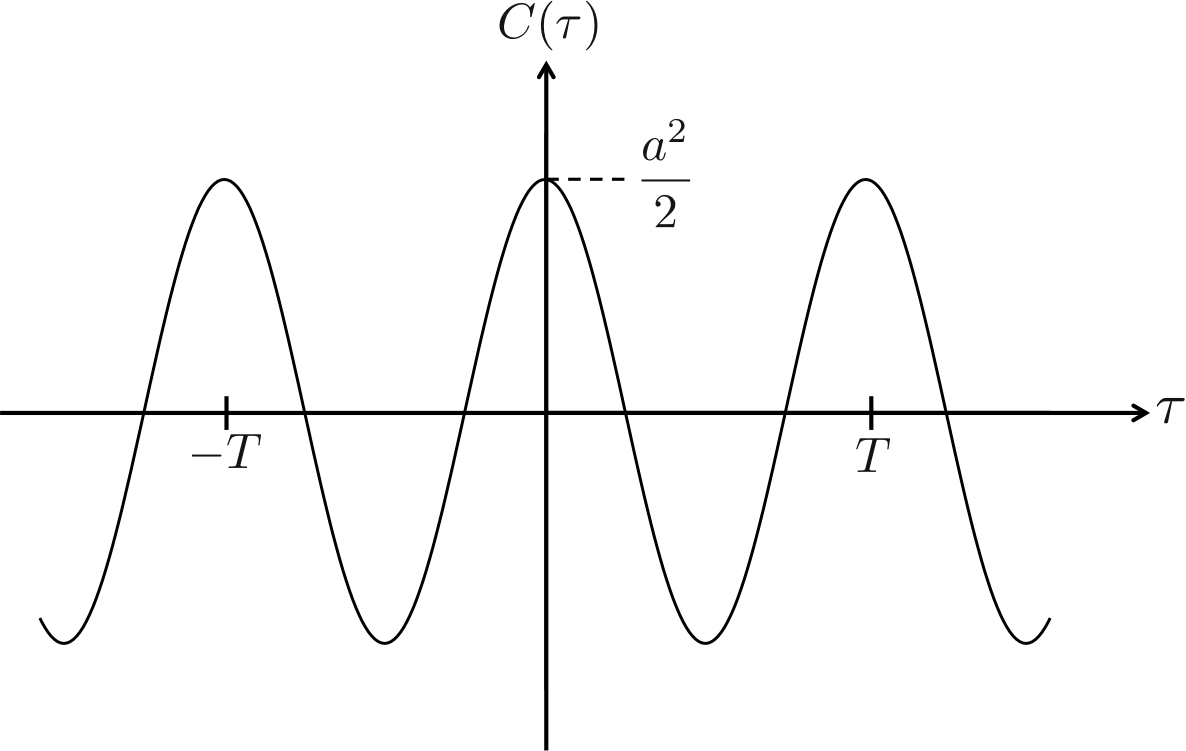
図2.

正弦波の自己相関関数を図に表すと図2となる。 やはり、予想したように\(\tau = nT \)の時に、自己相関関数が最も大きくなるということがわかるのである。 広告