スペクトルの概念

　フーリエ変換を理解する上でスペクトルと言う概念が非常に重要になってくる。 このスペクトルという概念を説明する上で、光のスペクトルを使って説明すると非常に理解が早い。 太陽光などの白色光には様々な波長の光が混じっている。 逆に言うと、様々な波長の光が混じっているから白く見えるのである。 この白色光を図1のようにプリズムに入射させる。

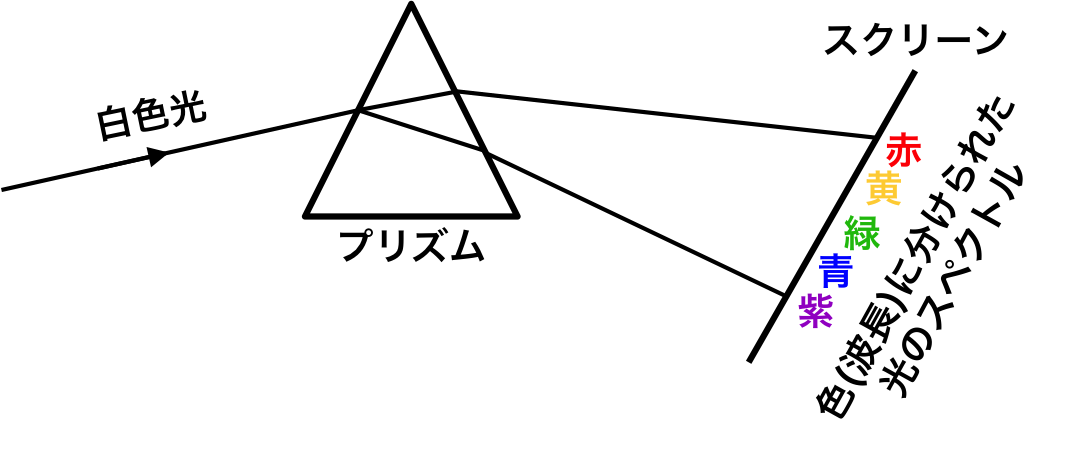
図1.

白色光は空気からガラスへと屈折率の異なるものに入射することになる。 この時、白色光に含まれるより波長の短い光は、より屈折をする。 そのためスクリーンには下から紫→青→緑→黄→赤の順で投影される。 （この時、光は連続スペクトルで現れるので、上の5色だけ見えるわけではない。） もし、スクリーンがCCDや光電子増倍管などの光の強さを検出できる機器であった場合、波長ごとの光の強さを検出することができる。 つまり、光のスペクトルを見ることで白色光中の各波長成分の光の強さの分布がわかるのである。

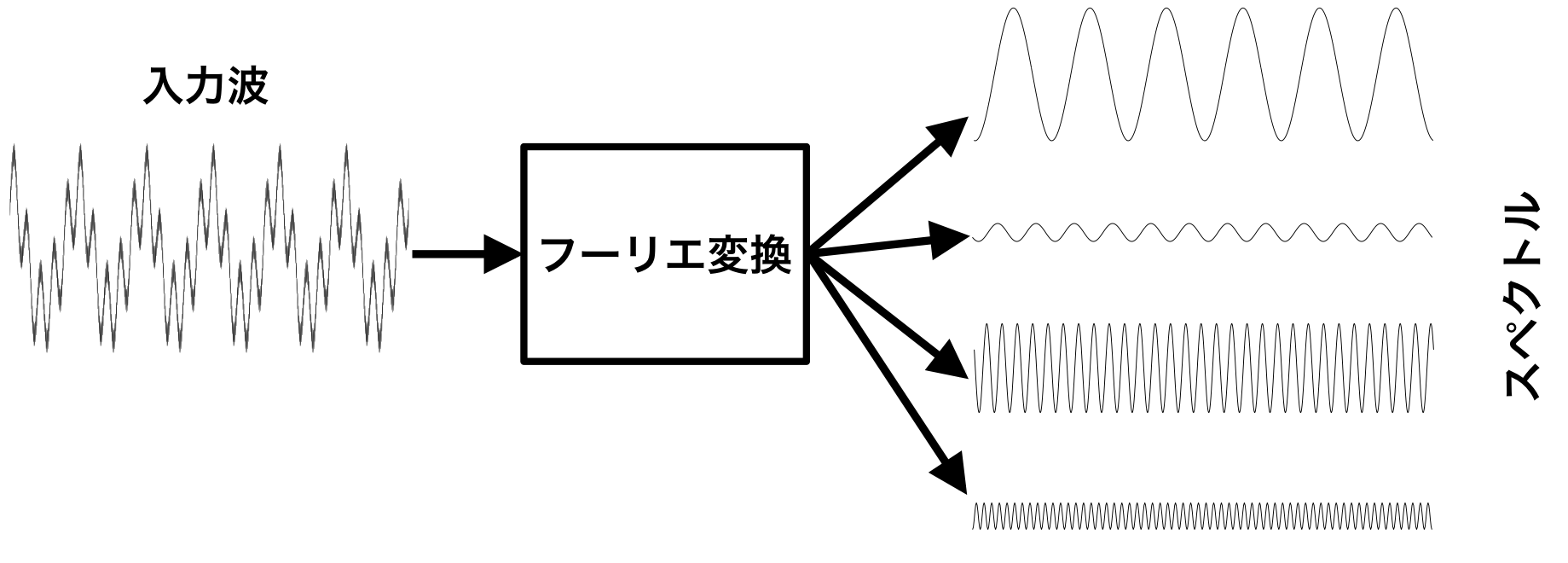
図2.

　このプリズムの役割を果たすのが、フーリエ変換である。 図2のように様々な波長が混ざり合っている波を入力波として、フーリエ変換を行う。 このフーリエ変換によって、それぞれの周波数ごとの振幅、位相がわかるのである。 繰り返しになるが、 \begin{eqnarray} x(t) &=& \frac{1}{\sqrt{2 \pi}} \int^{\infty}_{-\infty} X(\omega) e^{i \omega t}\ d\omega \ \ \ \ \ \ \ \ \ \ (1) \\ X(\omega) &=& \frac{1}{\sqrt{2 \pi}} \int^{\infty}_{-\infty} x(t) e^{-i \omega t}\ dt \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} で表される、\( X(\omega) \)を\( x(t) \)のフーリエ変換と呼ぶ。 この時、図2の入力波は\( x(t) \)に相当し、それぞれの周波数における\( X(\omega) \)は振幅を意味する。 このことから、\( |X(\omega)|^2 \)はその周波数におけるエネルギーを表している。 なぜエネルギーが振幅の2乗で表されるかは力学で学ぶ、調和振動子の力学的エネルギーを参考にして欲しい。
　以上をまとめると、フーリエ変換は、光におけるプリズムの役割を果たし、\( x(t) \)のスペクトルを得ることができる。 フーリエ変換で得られた各周波数成分のエネルギーは、 \begin{eqnarray} |X(\omega)|^2 = X(\omega)X^*(\omega)\ \ \ \ \ \ \ \ (3) \end{eqnarray} で表される。ここで、\( X^*(\omega)\)は\( X(\omega) \)の複素共役である。尚、周波数\( \omega \)とエネルギー\( |X(\omega)|^2 \)の分布の関係のことはエネルギースペクトルと定義されている。