フーリエ積分・フーリエ変換の意味
フーリエ級数の区間を\( [-T/2,\ T/2] \)から\( [-\infty,\ \infty]\)まで拡張することで、 \begin{eqnarray} x(t) &=& \frac{1}{\sqrt{2 \pi}} \int^{\infty}_{-\infty} X(\omega) e^{i \omega t}\ d\omega \ \ \ \ \ \ \ \ \ \ (1) \\ X(\omega) &=& \frac{1}{\sqrt{2 \pi}} \int^{\infty}_{-\infty} x(t) e^{-i \omega t}\ dt \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} を得るのである。 \( X(\omega) \)のことをフーリエ積分と言う。 また、\( X(\omega) \)を\( x(t) \)のフーリエ変換と呼ぶ。 \( X(\omega) \)と\( x(t) \)の詳しい導出方法は、フーリエ積分・フーリエ変換のページを見て欲しい。
ではこのページでは、フーリエ変換の意味について考えていこうと思う。 式(1)を使って式(2)の\( X(\omega)\)へフーリエ変換した場合は何が変わっているだろうか? \( x(t) \)は何らかのパラメーターの時間変化を示しているのに対して、\( X(\omega) \)は周波数の変数となっている。 式(1)に\( X(\omega)\)が含まれていることから考えて、\( X(\omega) \)は\(x(t)\)を三角関数の重ね合わせ(フーリエ級数)で表した時における、各周波数成分の振幅であると言える。図に示すと図1のような関係がある。
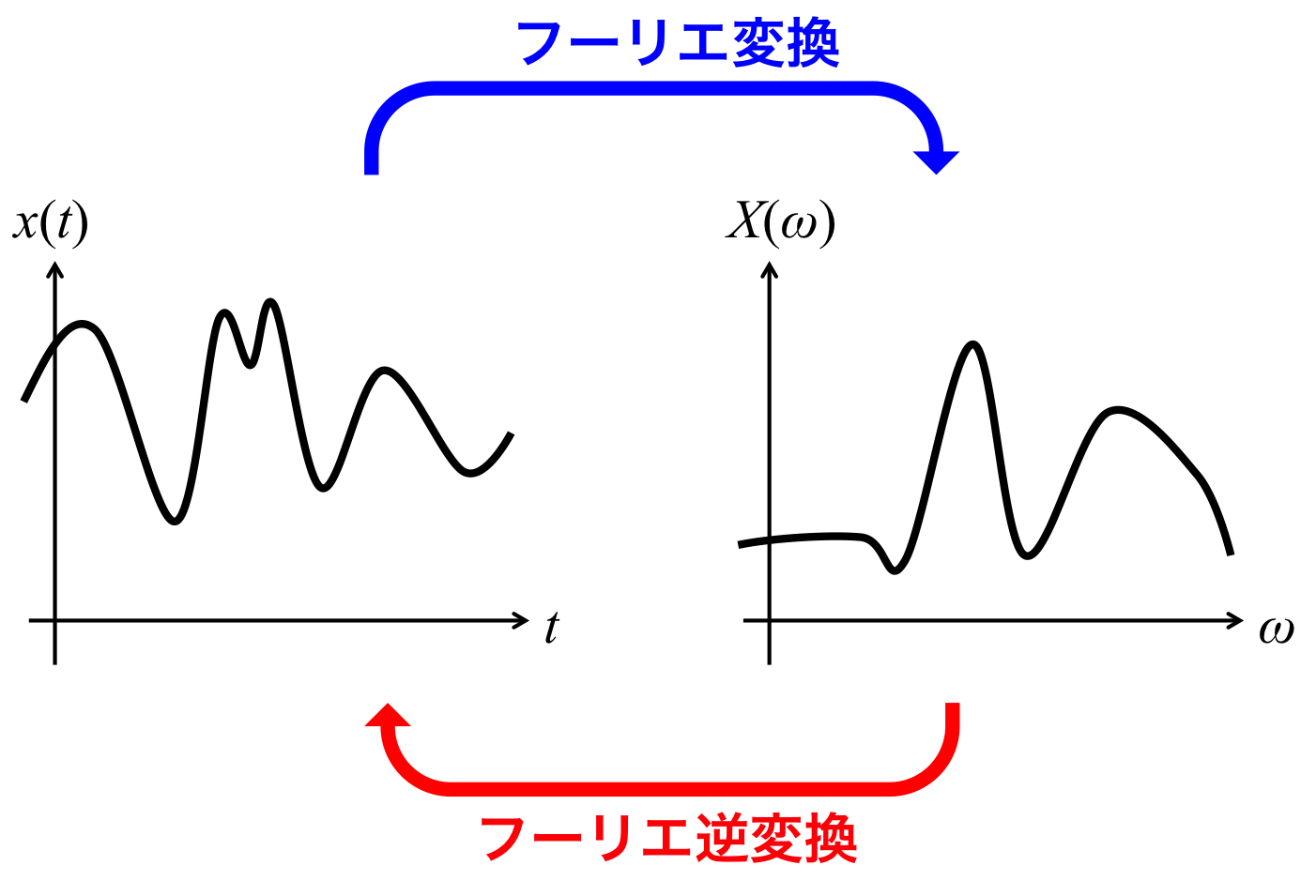
図1.