単位格子（単位胞）

格子点の位置を示すために基本並進ベクトル

\begin{eqnarray} {\bf R} = n_1 {\bf a_1} + n_2 {\bf a_2} + n_3 {\bf a_3} \end{eqnarray}

で与えられるのであった（\(n_1,\ n_2,\ n_3\)は整数）。

\( {\bf R} \)は\(n_1,\ n_2,\ n_3\)が整数であるため、3次元空間の任意の点を示すことができず、離散的な点を指し示す。

2次元空間で示すと図1のようになる。

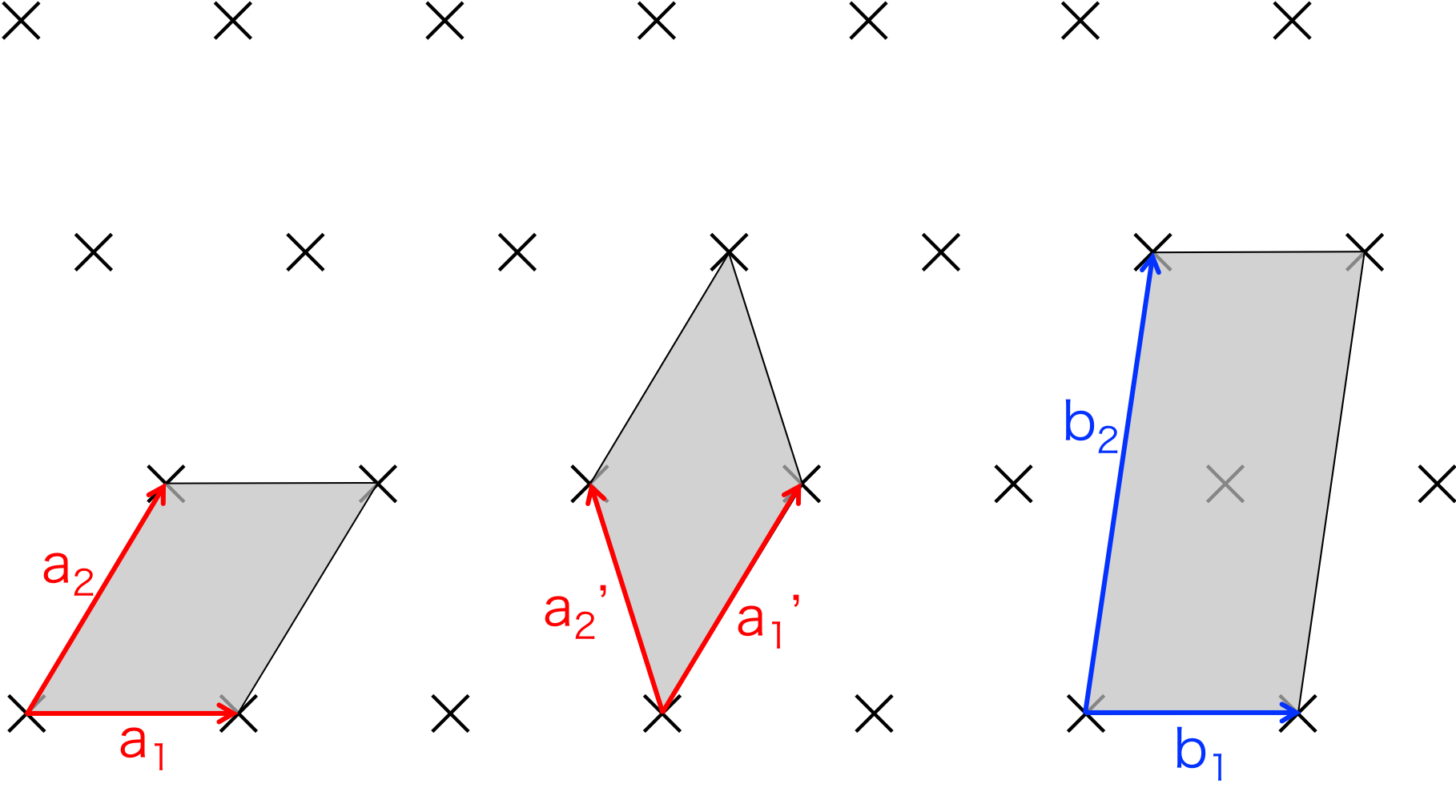
“fig1-1-1.png”
図1. \( {\bf R} \)で表される点。バツ印は格子点である。

この場合、左側に位置している\({\bf a_1}\)、\({\bf a_2}\)で囲われた平行四辺形のことを単位格子または単位胞と呼ぶ。

単位格子の選び方はただ1つに決まるわけではなく、もし

\begin{eqnarray} {\bf R} = n_1' {\bf b_1} + n_2' {\bf b_2} \end{eqnarray}

とした場合は右端のものが単位格子となるのである。

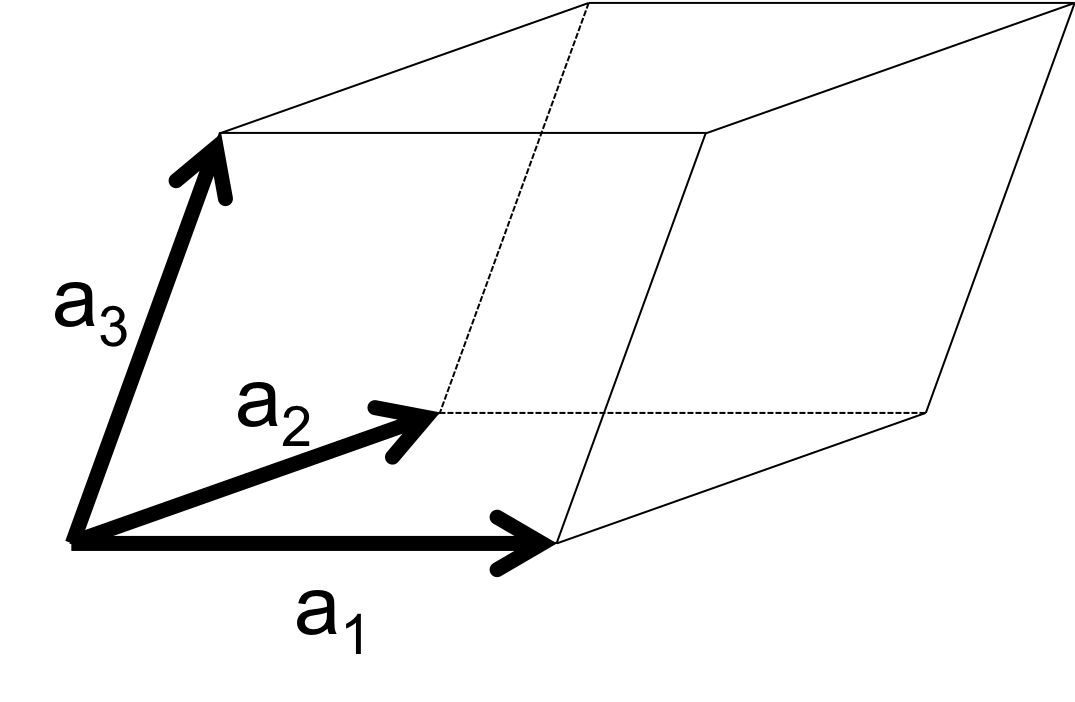
“fig1-2-2.png”
図2. 3次元の場合の単位格子

3次元の場合の単位格子が図2のように平行六面体となる。

また、単位格子の内部に格子点を含まないものを単純単位格子と呼び、単位格子の中に格子点を含むものを多重単位格子と呼ぶ。

つまり、図1の左端の単位格子は単純単位格子であり、右端の単位格子は多重単位格子となるのである。