基本並進ベクトル
カテゴリー:レーダー技術
結晶を学ぶ前に数学的な表現方法について説明しておく。
結晶とは単位格子の繰り返しによって作られている。
3次元空間内の任意の点を示す際には、以下のようにベクトルで表すことができる。
\begin{eqnarray} {\bf R} = u_1 {\bf a_1} + u_2 {\bf a_2} + u_3 {\bf a_3}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
この時、\( u_1 = n_1 \)、\( u_2 = n_2 \)、\( u_3 = n_3 \)として、\( n_1,\ n_2,\ n_3\)が整数であるとすると\( {\bf R}\)は 3次元空間の自由な場所を示すことができなくなり、ある飛び飛び(離散的な)点しか示すことができなくなる。
この時、\( {\bf R} \)で表される点を格子点と呼ぶ。
また、\( {\bf a_1},\ {\bf a_2},\ {\bf a_3}\)を基本並進ベクトルと呼ぶ。
基本並進ベクトルによって作られる平行六面体は単位構造と呼ばれる。
具体的に2次元空間に基本並進ベクトルと格子点を表すと図1のようになる。
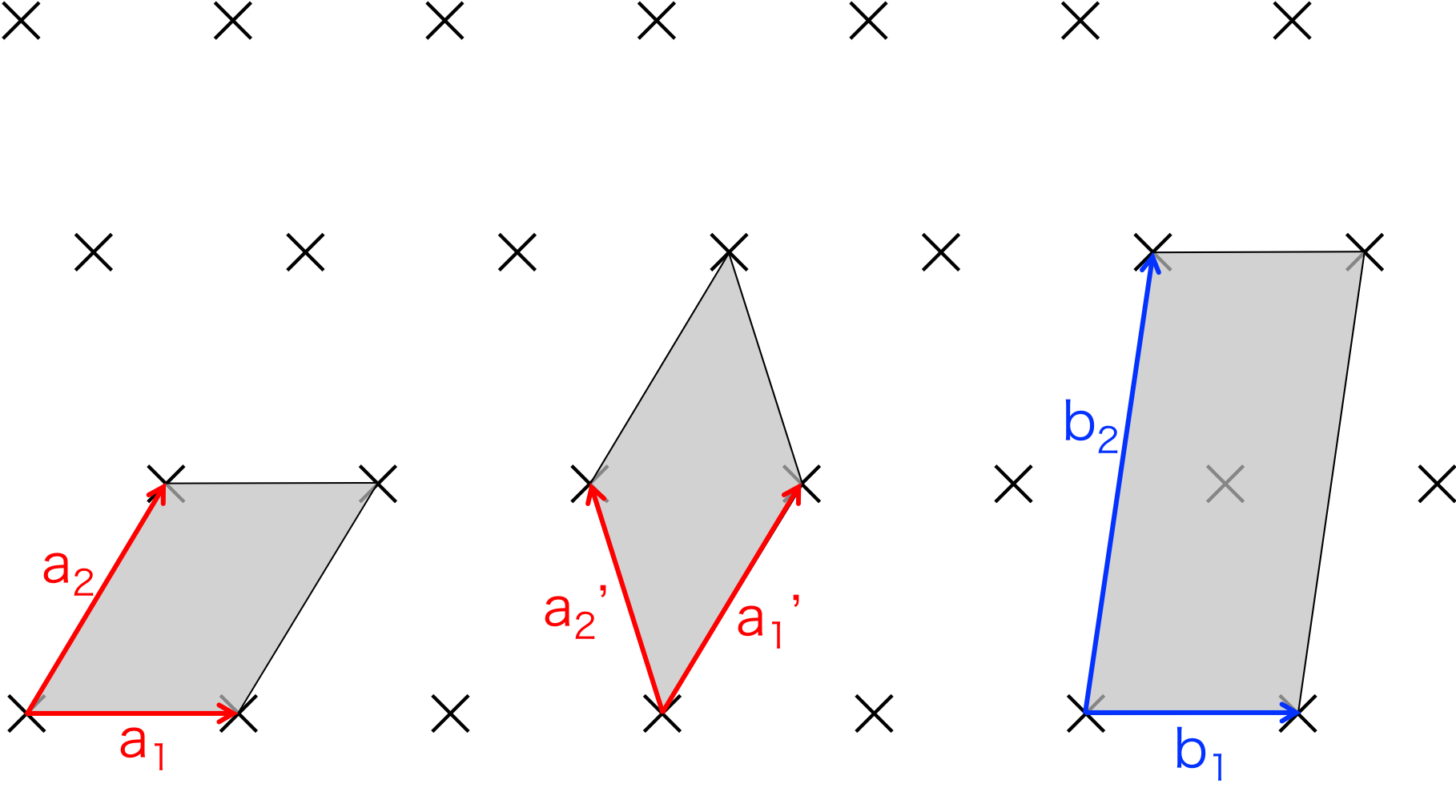
図1. \( {\bf R} \)で表される点。バツ印は格子点である。
基本並進ベクトル
\( {\bf a_1} \)と\( {\bf a_2} \)に対して、\( {\bf a_1}' \)と\( {\bf a_2}' \)は以下のような関係がある。
\begin{eqnarray} {\bf a_1}' &=& {\bf a_2} \\ {\bf a_2}' &=& {\bf a_2} - {\bf a_1} \end{eqnarray}
このことから、\( {\bf R} = n_1' {\bf a_1}' + n_2' {\bf a_2}' \)とすることができる (\(n_1'\)と\(n_2'\)は整数)。
従って、\( {\bf a_1}' \)と\( {\bf a_2}' \)は\( {\bf R}\)を与える基本並進ベクトルである。
\( {\bf R}\)を\( {\bf a_1} \)と\( {\bf a_2} \)で表した場合と、\( {\bf a_1}' \)と\( {\bf a_2}' \)で表した場合では ベクトルによって囲われる平行四辺形の面積が等しいという共通点があり、
\begin{eqnarray} \frac{1}{2}\sqrt{|x_1|^2|x_2|^2 - (x_1 \cdot x_2)^2} = \frac{1}{2}\sqrt{|x_1'|^2|x_2'|^2 - (x_1' \cdot x_2')^2} \end{eqnarray}
の関係がある。
しかし、\( {\bf b_1} \)と\( {\bf b_2} \)が作る平行四辺形はこれらの平行四辺形の面積とは異なるので、 \( {\bf b_1} \)と\( {\bf b_2} \)は\( {\bf R}\)を与える基本並進ベクトルではないのである。
ちなみに同じ\( {\bf R}\)を与える基本並進ベクトルを得る場合には、 ベクトルが作る平行四辺形の中に格子点が含まれないようにすれば良いのである。
世界最大級のオンライン学習サイトUdemy