指数関数（複素数）を使った波動の表し方

自然現象による変動成分をフーリエ解析することで、様々な周期の波動に分解できるのであった。この時一つの波動を表現するときに

\begin{eqnarray} Ae^{i( \omega t + \phi )}\ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

で表されることが多い。でも我々が高校の時に習った波の表し方は三角関数を使って

\begin{eqnarray} A \cos (\omega t + \phi )\ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

とすることが多かった。式(1)と式(2)の波の表し方は一体何がことなるのであろうか？実は、式(1)も式(2)も意味する波は同じである。しかし、式(1)のように指数関数と複素数を合わせて波を表した方が複雑な計算の際に非常に便利なので、式(1)の形が使われることが多い。ここではその理由を説明していこうと思う。

まず、式(1)をオイラーの公式を使って三角関数の展開すると

\begin{eqnarray} e^{i (\omega t + \phi) } = A \cos ( \omega t + \phi) + i A\sin (\omega t +\phi)\ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

となる。ここで式(2)に含まれている\( \cos ( \omega t + \phi )\)が出てきた。しかし、\( i \sin (\omega t + \phi)\)もくっついている。この\( \cos \omega t \)と\( \sin \omega t \)を図で表すと以下のようになる。

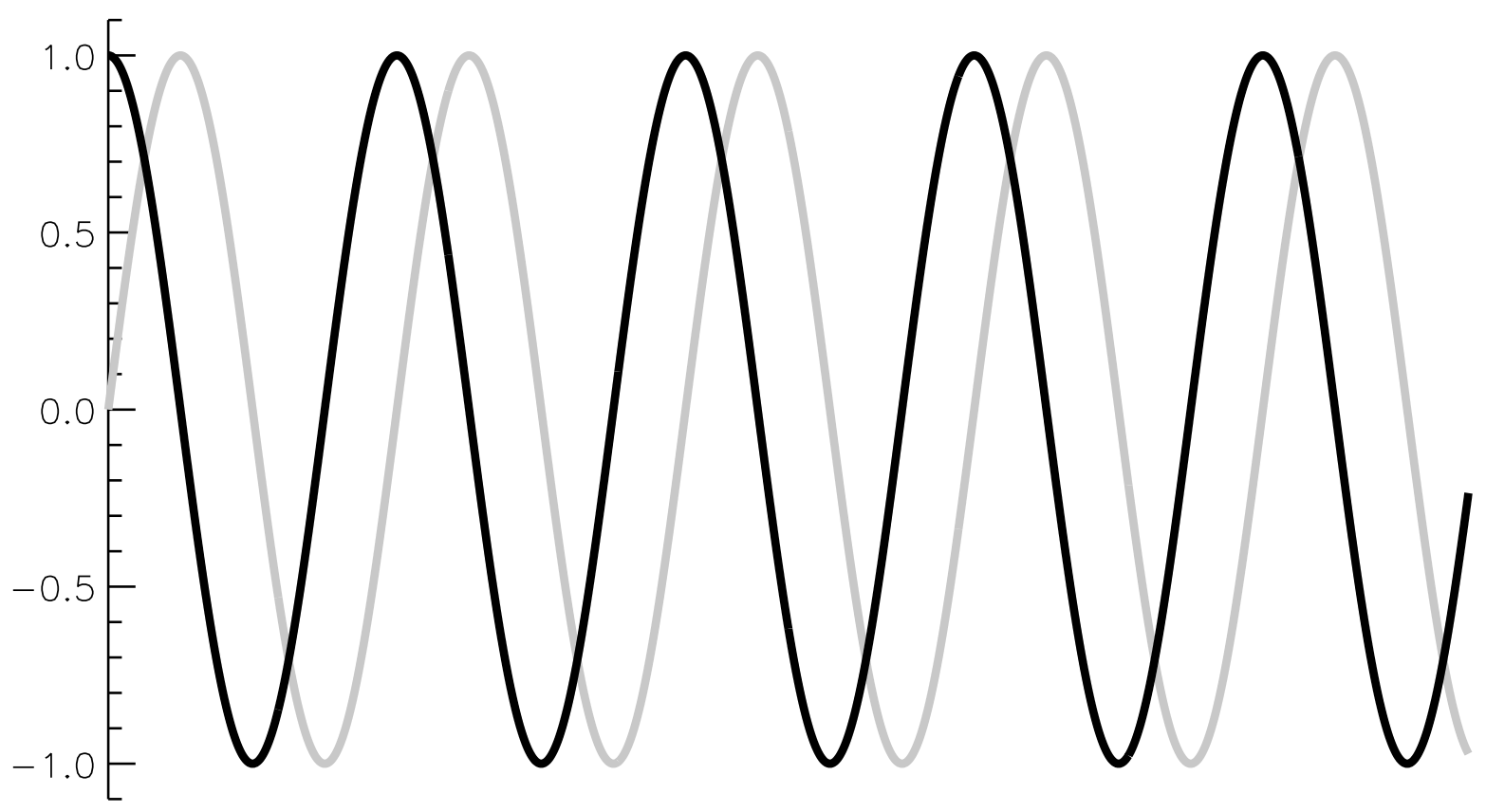
図1. \( \cos \omega t\)（黒色）と\(\sin \omega t \)（灰色）。\( \phi=0 \)で計算

2つ波動が出てきてしまったがまずは落ち着こう。実は、「自然現象を複素数で表した時、実部が観測される。」という決まりがある。そのため、\( e^{i(\omega t + \phi)} \)と\( \cos ( \omega t + \phi) \)は同じ波動を表していると言えるのである。

図1で考えると灰色の虚部の変動は観測されないので、黒の実線で表された実部の変動のみが観測されるのである。この決まりを使うことで、微分や積分でその形を変えることがない指数関数の方が三角関数より、波動を表す際に用いられるのである。

多くの教科書では、指数関数を波動を表す際に用いる理由としてここまでしか説明しない。しかし実はもっと大きな理由があるのである。それを説明してみようと思う。もう一度、指数関数を表してみる。

\begin{eqnarray} A e^{i(\omega t + \phi)} \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

ここで、Aは振幅である。式(3)では振幅を1としたが、ここでは振幅を考える。次に、指数関数を以下のように分解する。

\begin{eqnarray} Ae^{i\phi} e^{i(\omega t)} \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}

ここで、以下のように振幅を複素数に変換する。

\begin{eqnarray} \tilde{A} = Ae^{i\phi} = A \cos \phi + iA \sin \phi \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}

すると、位相\( \phi \)は以下のように表すことができる。

\begin{eqnarray} \tan \phi = \frac{\mathrm{Im}(\tilde{A})}{\mathrm{Re}(\tilde{A})} \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}

ここで、\( \mathrm{Re}(\tilde{A}) \)は\( \tilde{A} \)の実部、\( \mathrm{Im}(\tilde{A}) \)は\( \tilde{A} \)の虚部である。ここまでで分かったと思うが、指数関数で波動を表した場合、振幅を複素数とすることで位相も表現できるのである。このように、波動を指数関数で表すことのメリットは微分積分で形を変えないばかりか、位相を振幅で表現できるということも含まれるのである。