磁場に勾配がある場合の運動
カテゴリー:プラズマ物理学
磁場に勾配がある中を運動するプラズマはどのように運動するのだろう。 図1のようにy方向に行けば行くほど磁場が強くなる場合を考える。 まず、ラーモア半径(プラズマの円運動の半径)は
\begin{equation} r_L = \frac{mv_{\perp}}{|q|B}\ \ \ \ \ \ \ \ \ (1) \end{equation}
と表されることを思い出す。\(v_{\perp}\)は磁場に垂直なプラズマの速度成分である。 磁場が強くなればなるほどラーモア半径は小さくなっていく。
円運動している最中にラーモア半径に変化がなければプラズマはその場で円運動をしているだけであるが、 ラーモア半径が運動している最中に変化する場合は図1のようにドリフトをすることが想像できる。
磁場中のプラズマの旋回中心のドリフト速度\( {\bf v}_f \)はプラズマにかかる力\( {\bf F} \)を用いて、
\begin{equation} {\bf v}_{f} = \frac{1}{q} \frac{{\bf F} \times {\bf B}}{B^2} \ \ \ \ \ \ \ \ \ \ (2) \end{equation}
で与えられる。磁場に勾配がある場合にプラズマにかかる力\( {\bf F} \)を求めることで、このプラズマがどのような運動をするのか明らかにしていく。
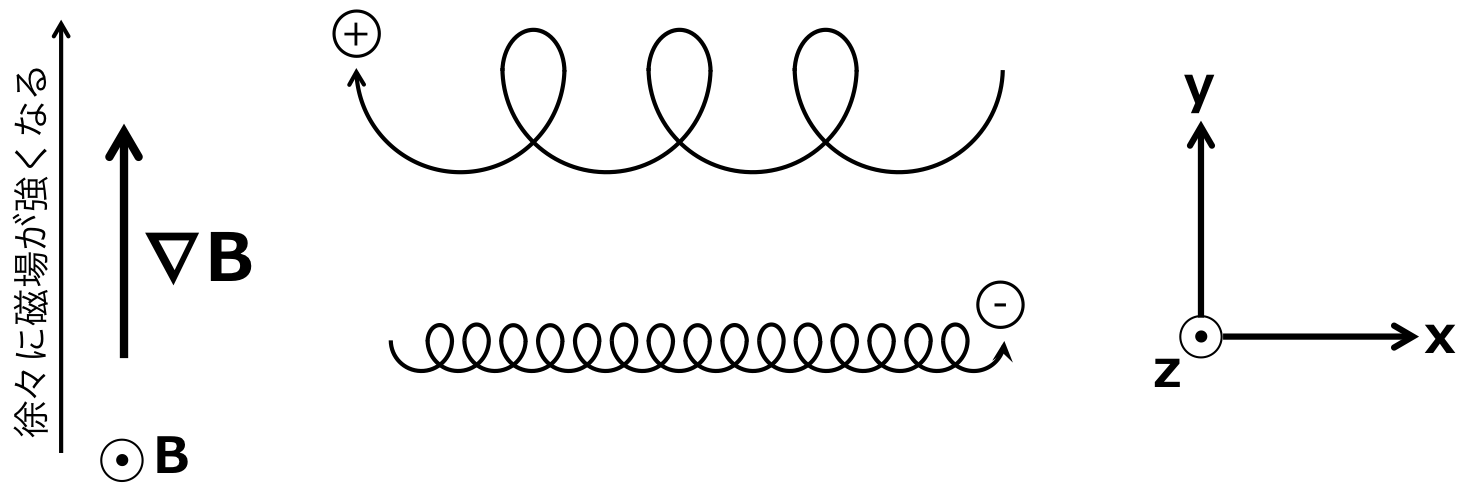
図1 磁場に勾配がある場合のプラズマの運動
では図1に戻って運動方程式からどのようにドリフトをするのかを考えていく。
図1のように磁場がz方向にかかっており、y方向に行けば行くほど強くなる場合を考える。 (ちょっとややこしいが、yの正の方向に行けば行くほど、より強いz方向の磁場がかかっているという意味である。) この時、プラズマの運動方程式を記述すると、
\begin{equation} \mathrm{{\bf F}} = q {\bf v} \times {\bf B}\ \ \ \ \ \ \ \ \ (3) \end{equation}
となる。各成分に書き直すと
\begin{eqnarray} F_x &=& q v_y B_z(y) \ \ \ \ \ \ \ \ \ (4) \\ F_y &=& - q v_x B_z(y) \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
となる。ここで、プラズマのラーモア半径と比べて磁場の勾配が非常に緩やかであった場合を想定する。 (プラズマが一回転するくらいの領域では磁場はほとんど変わらないと仮定する。)
すると、プラズマの速度は一様な磁場の中のプラズマの速度と同じと近似することができて、
\begin{eqnarray} v_x &=& v_{\perp} \cos \omega t \ \ \ \ \ \ \ \ \ (6)\\ v_y &=& \pm v_{\perp} \sin \omega t \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
を用いることができる。ここで、\( \omega \)はジャイロ周波数で\( \omega = qB/M \)である。 \( v_x,\ v_y\)を式(3)と式(4)に代入すると、
\begin{eqnarray} F_x &=& \pm q v_{\perp} \sin (\omega t) B_z(y) \ \ \ \ \ \ \ \ \ (8) \\ F_y &=& - q v_{\perp} \cos (\omega t) B_z(y) \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}
を得る。 次に磁場の変化量を方程式に与えるために、磁場をテイラー展開する。 磁場のテイラー展開は3変数のテイラー展開として解けて、
\begin{eqnarray} {\bf B} &=& {\bf B}_0 + \left( {\bf r} \cdot \nabla \right){\bf B} + \frac{ \left( {\bf r} \cdot \nabla \right)^2 }{2}{\bf B} + \cdots \\ B_z &=& B_0 + y \frac{\partial B_z}{\partial y} + \frac{1}{2}y^2 \frac{\partial^2 B_z}{\partial y^2} + \cdots \end{eqnarray}
とできる。3次以降は非常に小さくなるので、無視する。 これを、式(7)、(8)に代入すると、
\begin{eqnarray} F_x &=& \pm q v_{\perp} \sin (\omega t) \left( B_0 \pm r_L (\cos\omega t) \frac{\partial B_z}{\partial y} \right) \ \ \ \ \ \ \ \ \ (10) \\ F_y &=& - q v_{\perp} \cos (\omega t) B_z(y) \left( B_0 \pm r_L (\cos\omega t ) \frac{\partial B_z}{\partial y} \right) \ \ \ \ \ \ \ \ \ (11) \end{eqnarray}
を得る。\( y = \pm r_L \cos\omega t \) を使っている。
これによって、磁場勾配がある中でのプラズマにかかるx方向とy方向の方程式を得ることができた。 ここで、気をつけなくてはならないのは、磁場中に置かれたプラズマは回転運動しているということである。 回転運動している場合にプラズマの旋回中心にかかる力を求めるためには、1回転する間に受ける力を平均する必要がある。 (半回転で右方向に力を受けて、もう半回転で同じ分だけ左に力を受けた場合、1回転平均すると力をつけていないことになる。) 1回転は\(t\)が\( 0 \rightarrow 2 \pi \)した時である。 よって、式(7)、(8)を0から\( 2 \pi \)で積分して、\(2\pi\)で割る。 つまり、
\begin{eqnarray} \bar{F_x} &=& \frac{1}{2 \pi} \int_0^{2\pi} F_x\ dt = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \\ \bar{F_y} &=& \frac{1}{2 \pi} \int_0^{2\pi} F_y\ dt = \mp \frac{1}{2} qv_{\perp}r_L \left( \frac{\partial B_z}{\partial y} \right) \ \ \ \ \ \ \ \ \ (13) \end{eqnarray}
を導ける。これを式、(2)に代入することで
\begin{equation} v_{f} = \frac{1}{q} \frac{\bar{F_y}}{B}{\bf i} = \mp \frac{1}{2} \frac{v_{\perp} r_L}{B} \left( \frac{\partial B}{\partial y} \right){\bf i} \ \ \ \ \ \ \ \ \ (14) \end{equation}
となる。ここで、\({\bf i}\)はx方向の単位ベクトルである。(外積の計算の際に出現) これをもっと一般的に書き直すと、
\begin{equation} {\bf v}_{f} = \pm \frac{1}{2} v_{\perp} r_L \frac{{\bf B} \times \nabla B}{B^2}\ \ \ \ \ \ \ \ \ (15) \end{equation}
を得る。やはり、磁場に勾配がある場合は磁場と磁場配ベクトルに垂直な方向にドリフトするのである。
\( \pm \)の記号は電子とイオンの場合を示しており、磁場勾配によるドリフト運動の場合、イオンと電子は逆方向にドリフトする。 これによって、電流が流れるのである。
このとき、\( v_{\perp} \)は旋回中心の速度ではなく、プラズマ粒子1つの磁場に対して垂直な速度であることに注意する。 このようなドリフトはgrad Bドリフト(グラッドBドリフト)、または磁場勾配ドリフトと呼ぶ。