行列式
逆行列を求める際に、逆行列が存在するかどうかをまず確かめる。
この際に使用するものが判別式で、以下のような2行2列の行列
\[
A=
\left(
\begin{array}{cc}
a & b \\
c & d
\end{array}
\right)\ \ \ \ \ \ \ \ \ \ \ \ \ (4.6.1)
\]
の判別式\(\mathrm{det} A\)は
\begin{equation}
\mathrm{det} A = ad - bc\ \ \ \ \ \ \ \ \ \ \ \ \ (4.6.2)
\end{equation}
で表せる。この判別式を求めるために行列式を使うと非常に分かりやすく便利である。
行列\(\mathrm{det} A\)の行列式は行列のカッコを直線に変えたもので、
\[
\mathrm{det}A = |A| = \left|
\begin{array}{cc}
a & b \\
c & d \\
\end{array}
\right|\ \ \ \ \ \ \ \ \ \ \ \ \ (4.6.3)
\]
で表される。逆行列の判別式と等しいので、行列\( A \)は正方行列でないといけない。
行列式の計算方法は対角線の値を掛け合わせて引けば良いのである。
視覚的に行列式の計算方法を示したものを図4-6-1に示す。

図4-6-1 行列式の計算方法
まず、左上から右下への対角線上にある数値(赤)を掛け合わせ、右上から左下への対角線上にある数値を掛け合わせた値(青)を引いたものが\(\mathrm{det} A \)である。
ここまでは非常に簡単である。3行3列の行列式になると途端に複雑になり始める。
行列Aが
\[
A=
\left(
\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}
\right)\ \ \ \ \ \ \ \ \ \ \ \ \ (4.6.4)
\]
の3行3列で表されるとき、行列式は
\[
\mathrm{det}A = |A| = \left|
\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}
\right| = a_{11} a_{22} a_{33} + a_{21} a_{32} a_{13} + a_{31} a_{12} a_{23} - a_{11} a_{32} a_{23} - a_{31} a_{22} a_{13} - a_{21} a_{12} a_{33} \ \ \ \ \ \ \ \ \ \ \ \ \ (4.6.5)
\]
と計算できる。対角を計算する法則は2行2列のときと変わらない。
計算方法を視覚的に表したものを図4-6-2に示す。
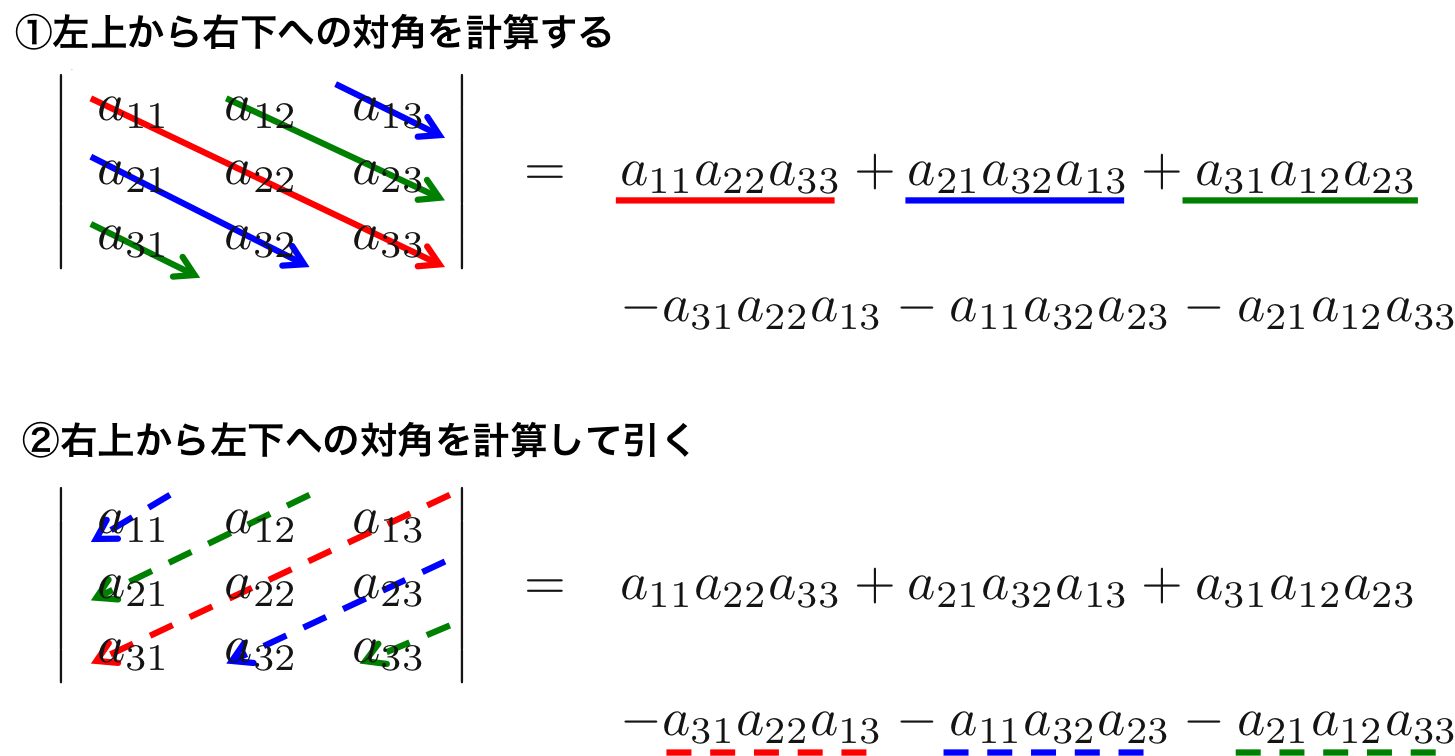
図4-6-2 3行3列の行列式の計算方法
一見難しそうに見えるが、2、3例行列式を解けばその法則性を理解することができるだろう。
行列式は判別式を求めるためだけに利用されるのではなく、
固有値問題や、ベクトル演算子の計算でよく行列式は使われる。
広告

