運動座標系(並進運動)
並進運動
これまでの座標系は特に動いたりはしなかったが、ここでは座標系が動く場合を考える。 普段は質点などが運動していたが、運動と同じ速さで座標系が動けば、その質点(物質)は運動している座標系に固定されて考えることができる。 つまり、質点の運動が様々な成分を持っている場合は、その一つの成分を消して単純化できるという点で便利である。 空間に固定された座標系\( O-xyz \)を考える。 次にこの固定された座標系に対して、並進運動(すべての点が平行に移動)をしている座標系\( O’-x’y’z’ \)系を考える(図3-16)。 \( t=0 \)で\( O-xyz \)と\( O’-x’y’z’ \)は一致しており、その後、\(x\)軸、\(y\)軸、\(z\)軸はそれぞれ、\(x’\)軸、\(y’\)軸、\(z’\)軸と平行を保ったまま運動していくとする。 運動している動点\( P(t) \)の位置ベクトルを座標系\( O-xyz \)で表すと、\({\bf r}(t)\)、座標系\( O’-x’y’z’ \)で表すと、\({\bf r}’(t)\)であるとする。座標系\( O-xyz \)からみた座標系\( O-x’y’z’ \)の原点の位置ベクトルを\({\bf r}_0(t)\)とすれば、 \begin{equation} {\bf r}(t) = {\bf r}’(t) + {\bf r}_0 (t) \end{equation} の関係であることがわかる。 よって速度と加速度は \begin{eqnarray} \dot{\bf r}(t) &=& \dot{\bf r}’(t) + \dot{\bf r}_0(t) \\ \ddot{\bf r}(t) &=& \ddot{\bf r}’(t)+ \ddot{\bf r}_0(t) \end{eqnarray} と表される。もっとわかりやすく表現すれば、 \begin{eqnarray} {\bf v}(t) &=& {\bf v}’(t)+ {\bf v}_0(t) \\ {\bf a}(t) &=& {\bf a}’(t)+ {\bf a}_0(t) \end{eqnarray} となる。\(x,\ y,\ z\)軸はそれぞれ\(x’,\ y’,\ z’\)軸と平行であるので、2つの座標系でベクトルの成分は変わらない。 もし、座標系\( O-x’y’z’ \)が等速で運動している場合、\( {\bf v}_0 \)は定ベクトルとなり、 \begin{equation} {\bf r}(t) = {\bf r}’(t)+{\bf v}_0 t \end{equation} となる。つまり、 \begin{equation} {\bf a}(t) = {\bf a}’(t) \end{equation} である。つまり、固定された座標系と等速運動している座標系においてニュートンの運動方程式 \begin{equation} {\bf F} = m {\bf a} \end{equation} は常に等しい。このような、固定座標系から等速運動する座標系への変換をガリレオ変換という。 ガリレオ変換によって、ニュートンの運動方程式が変化しないことをガリレオ不変性という。
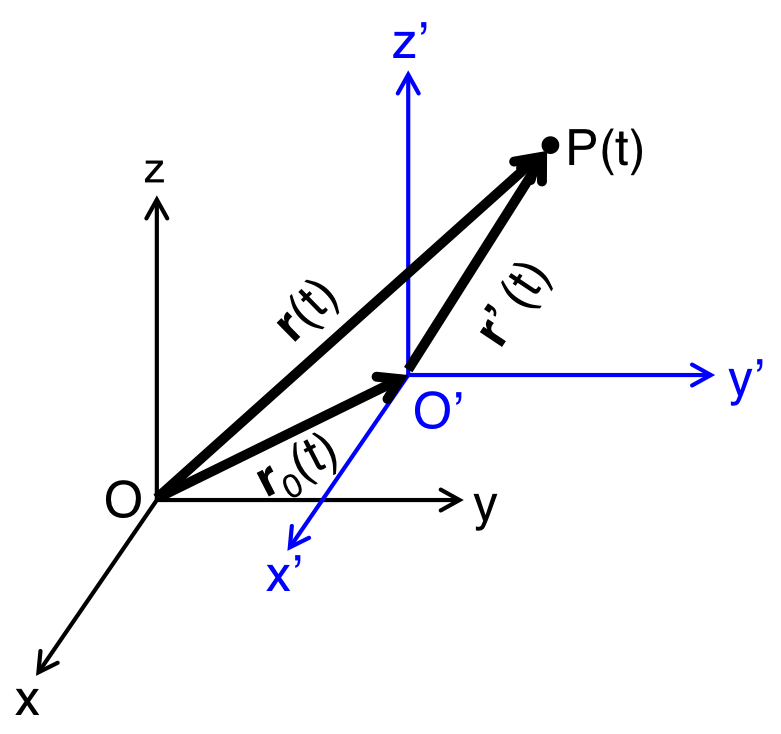
図3-19 空間に固定された座標と並進運動する座標