曲率と曲率半径
物体が曲線上を運動をしている時、ごく短い間の運動の軌跡は円で近似できる。 近似された円の半径を曲率半径といい、曲率半径の逆数をその運動の曲がり具合として、曲率という。 そのことから少しだけ、物体の運動から曲率と曲率半径について想像してみる。 自転車で走っている場面を想像してみて、急激に曲がった場合を考える。 この急激な動きは、その時間だけものすごく小さい円の上を運動していたと考えることができる。 つまり、急激に運動の方向を変えた場合の曲率半径は小さく、曲率は大きくなる。 次に、自転車で走っていて、グランドに大きな円を描くようにゆっくりと回った場合はどうだろうか? この時はグラウンドいっぱいに描けるくらいの円上を運動していることと近似できるわけであるから、その曲率半径は大きく、曲率は小さい。 では、ちょっとひねくれた考えをしてみて、ほとんどまっすぐ走っている場合はどうだろうか? この時はもはや地球上に描ける円では近似できず、例えば宇宙一杯に描くことができる円(地球上ではほとんど直線)の上を走っていると近似することができるくらいである。 この場合の曲率半径は宇宙の大きさくらいとなるのであるが、でかすぎてほぼ無限大である。曲率は、ほとんど0である。 以上のことをまとめると、
1. 曲率が大きい運動は急激に運動の方向が変化している。
2. 曲率がどの時間で計算しても一定である場合、その物質は円の上を運動している。
3. 曲率が0の場合、その物質は直線上を運動している。
と言える。では実際に曲率と曲率半径の求め方を説明していく。
図3-13に示すような曲線上を運動する質点を考える。質点はある時間\(t \)にP点におり、微小時間\( \Delta t \)後に点Qまで運動する。 Oは原点で、原点Oから点Pと点Qまでのベクトルは時間\(t \)の関数として \begin{eqnarray} \vec{OP} &=& {\bf r} (t) \\ \vec{OQ} &=& {\bf r} (t + \Delta t) \end{eqnarray} と表すことができる。点Pから点Qまでのベクトル\( \Delta r \)は \begin{equation} \vec{PQ} = \vec{OQ}- \vec{OP} = \Delta {\bf r} = {\bf r} (t+ \Delta t) - {\bf r}(t) \end{equation} となる。
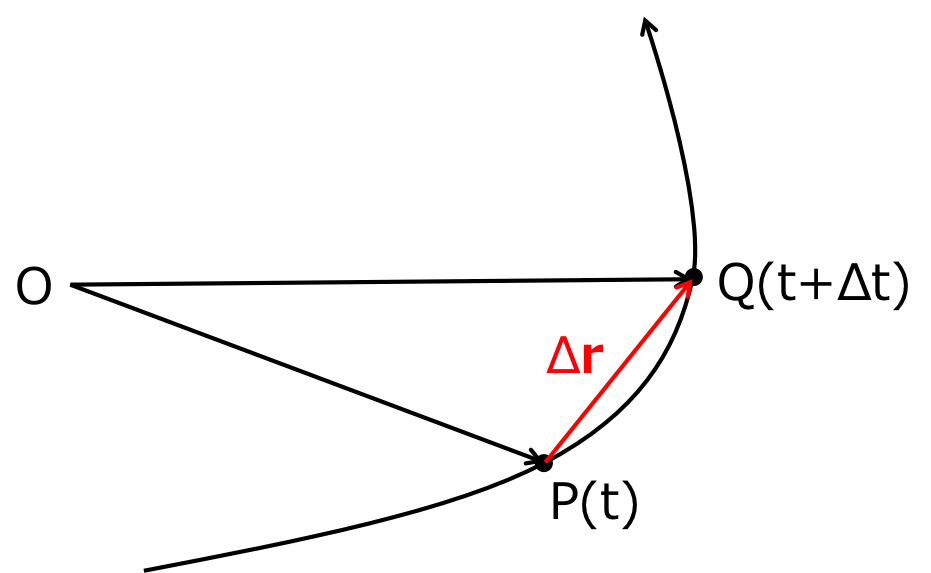
図3-13 質点の運動
\( \Delta t \)が限りなく小さくなった場合、点Pから点Qへの運動は図3-14のように円上(点線上)を運動していると近似できる。 円の中心はMとする。ここで、円の弧PQ(点Pから点Qまでの点線)は微小時間\( \Delta t \)が限りなく0に近づいた場合、\( \Delta {\bf r} \)と一致する。 弧PQの長さは中心Mの半径\( R \)を使って\( R \Delta \theta \)と書くことができる。 よって \begin{equation} \lim_{\Delta t \to 0} \frac{\Delta r}{R \Delta \theta} = \frac{dr}{Rd\theta} = 1 \end{equation} より、 \begin{equation} R = \frac{dr}{d\theta} \end{equation} と表すことができる。
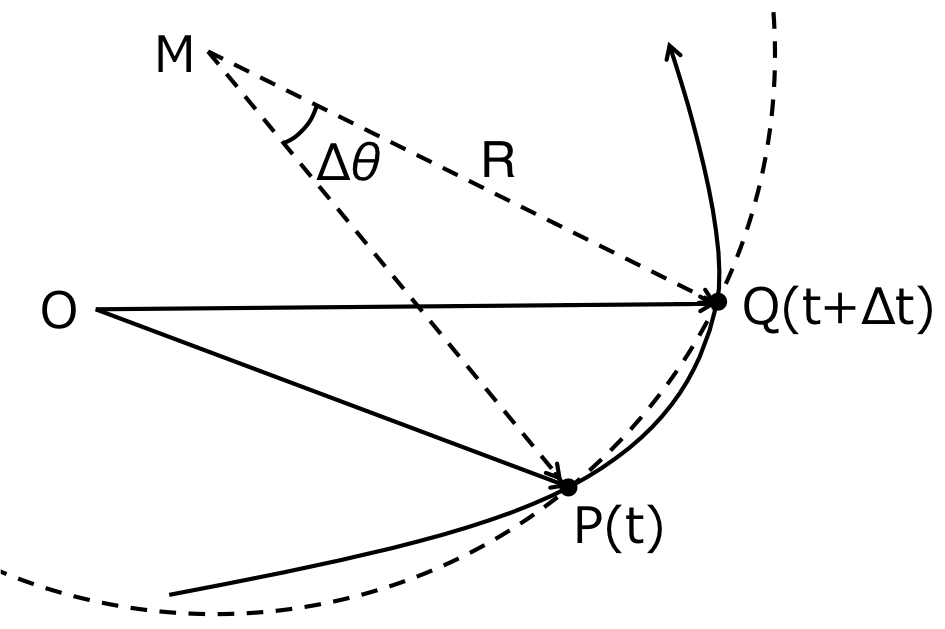
図3-14 質点の運動(円上を運動していると近似した場合)。Oは原点、Mは円の中心。
この式では\( \theta \)の時間変化量を求めることができれば曲率半径を求めることができるのだが、 そもそも\( \theta \)は与えられていない。よって、\(x\)と\(y\)だけで曲率半径を求める様にする必要がある。 \( \theta \)の変化をわかりやすく示すと図3-14の様になる。点Pの接線とある直線の成す角を\( \theta \)とすると、 そこから\( \Delta t \)進んだ点Qでの接線と直線との成す角は\( \theta + \Delta \theta \)である。 \( \Delta t \)が限りなく0に近づくと点Qでの接線と直線との成す角は\( \theta + d \theta \)となる。

図3-15 接線との関係
ここで、\( \tan \theta \)は \begin{equation} \tan \theta = \frac{dy}{dx} \end{equation} と表すことができる。これは点Pでの傾きが\( \tan \theta \)であると考えるとわかり易い。 点Pから微小時間進んだQ点での傾き\( \tan (\theta + d \theta) \)は \begin{equation} \tan (\theta + d \theta) = \frac{dy}{dx} + \frac{d}{dx} \left( \frac{dy}{dx} \right) dx \end{equation} と表すことができる。この上式と\( \tan \)の加法定理、 \begin{equation} \tan (\theta + d \theta ) = \frac{\tan \theta + \tan d\theta}{1-\tan \theta \tan d\theta} \end{equation} を用いて、以下の関係式を導くことができる。 \begin{equation} \frac{\tan \theta + \tan d\theta}{1-\tan \theta \tan d\theta} = \frac{dy}{dx} + \frac{d^2y}{dx^2} dx \end{equation} \(d\theta << 1\)であることを用いると\( \tan d \theta \approx d\theta \)とできるので、 上式は \begin{equation} \frac{\tan \theta + d\theta}{1-\tan \theta d\theta} = \frac{dy}{dx} + \frac{d^2y}{dx^2} dx \end{equation} となる。\( d \theta \)について解けば、 \begin{equation} d\theta = \frac{\frac{d^2y}{dx^2}}{1+\left( \frac{dy}{dx} \right)^2} dx \end{equation} を得る。この関係式と \begin{equation} dr = \sqrt{(dx)^2 + (dy)^2} = \sqrt{1 + \left( \frac{dy}{dx} \right)^2} dx \end{equation} の関係式を曲率半径を求める式に代入することで、以下の様に曲率半径を求める関係式を導出することができる。 \begin{eqnarray} R = \frac{dr}{d\theta} = \frac{\left( 1+ \left( \frac{dy}{dx} \right)\right)^{\frac{3}{2}}} {\frac{d^2y}{dx^2}} \end{eqnarray} 以上より、ある関数の1階微分と2階微分を計算することができれば、その関数の曲率半径を求めることができる。 この公式は非常に有用であるので、導出方法から理解しながら覚えておくと良い。 最後に曲率\( \kappa \)は \begin{equation} \kappa = \frac{1}{R} \end{equation} で与えられる。